De Investigación (EXTRA), propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 300.-

Dado el triángulo ABC, y las cevianas arbitrarias AA´, BB´ y CC´, desde los vértices A, B y C,  a los lados BC, AC y AB, respectivamente.

Sobre la ceviana AA´, (lo mismo para las demás), hacemos la siguiente construcción:

Desde A´, llevamos a su derecha e izquierda, la misma cantidad fija -pueden ser distintas, para B´, y C´-,para obtener sobre el lado BC, los puntos A'(B) y A'(C).

Por A, trazamos la paralela a BC, y por A'(B) y A'(C) la paralela, a AA', respectivamente. De esta forma obtenemos el paralelogramo A'(C)A'(B)A*(B)A*(C), y los similares, para BB´y CC´, respectivamente.
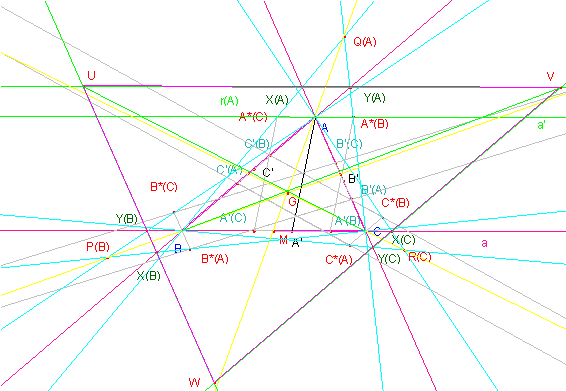
                Definimos los siguientes puntos por los pares de rectas que contienen a los dos segmentos que se indican:

X(A) =B A*(C)∩AC, Y(A)=   CA*(B) ∩AB, y, lo mismo X(B), Y(B), X(C), Y(C), para los otros dos vértices. 

Por último construimos las dos ternas de  puntos Q(A)= BA*(C) ∩ CA*(B),  P(B), y R(C), de forma análoga.

Y la terna de puntos, U= X(A)Y(A)∩X(B)Y(B),  V = X(A)Y(A)∩X(C)Y(C) y W = X(B)Y(B) ∩X(C)Y(C).  

Se pide: a) Demostrar que los puntos Q(A), P(B) y  R(C), están en las medianas
correspondientes a los vértices, A, B y C. (rectificado el 1 de marzo de 2006)

b) Hallar los lugares geométricos de los puntos Q(A), P(B) y R(C) cuando A' , B', y C' recorren los lados BC, AC y AB.

c) Demostrar que el triángulo UVW es homotético al triángulo ABC. Calcular el centro y la razón de la homotecia.

Romero, J.B. (2005): Comunicación personal.

Solución deSaturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca

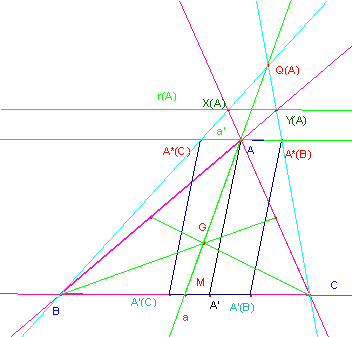
a) Veamos que el punto Q(A) yace en la mediana desde A.

Si consideramos este punto como vértice de la proyección de la recta a’=A*(B)A*(C) sobre la recta a= BC tenemos que el punto común A_∞ (el punto del infinito, por ser paralelas) es fijo: se proyecta en sí mismo. El vértice A es el punto medio del segmento A*(B)A*(C); su cuarto armónico es, por tanto A_∞. La proyección conserva la razón doble y por ello la cuaterna armónica (A*(B), A*(C), A, A_∞) se transforma en otra cuaterna armónica (C, B, M, A_∞), lo cual implica que M -proyección de A desde Q(A)- sea necesariamente el punto medio de BC, y por tanto Q(A) pertenece a la mediana.

b) Cada punto A’ (fijado un segmento a ambos lados) sobre BC induce un punto Q(A) sobre la mediana. Por tanto al variar éste sobre el lado el punto asociado recorre la mediana. Así pues el lugar geométrico buscado es la propia mediana (la recta completa, no el segmento). En el caso límite en que A’= A_∞, el punto definido es M. (Y también si A’ fijo y el segmento alrededor de él tiene longitud infinita).

c) Si el punto Q(A) está en la mediana ya hemos visto en problemas anteriores (nº 68) que sus proyecciones desde los vértices B y C sobre los lados, puntos X(A) e Y(A), están sobre una recta paralela a la base BC. Como esta recta contiene los vértices UV resulta que el triángulo UVW tiene sus lados paralelos al triángulo CBA, siendo por ello homotéticos.

El dibujo completo queda según puede verse en la última figura: