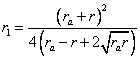Problema 301: En el triángulo ABC (<A=90º), construir el círculo (O₁, r₁) tangente externamente a los excírculos (I_b) e (I_c) de tal forma que sea también tangente al lado BC, con el punto de tangencia entre B y C.

Probar que: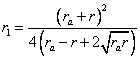

Donde: r_a= radio del excírculo (I_a) y r = inradio de ABC.

Solución de Juan Carlos Salazar, profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz)

:

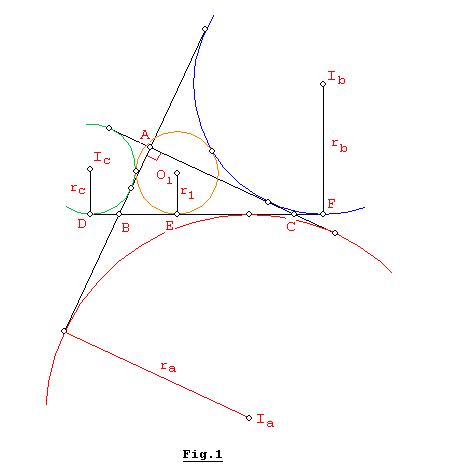
Si D, E, F son los puntos de tangencia de los circulos (I_c, r_c), (O₁, r₁), (I_b, r_b) con BC respectivamente, ver Fig.1, tenemos por simple cálculo: y . También DF = DE + EF = = b + c, de donde:

... (1)

Además como el triángulo ABC es recto en A, tenemos que:

b + c = a +2r… (2)

r_b.r_c = r.r_a… (3)

a = r_a - r… (4)

r_a –r = r_b + r_c… (5)

De (2) y (4): b + c = r_a + r

Reemplazando este resultado con (3) y (5) en (1) obtenemos: