Problema 303 de triánguloscabri
|
| Una generalización del problema 137 |
|
Luigi Cremona en el nº 217 de la página 180 de la edición inglesa de
su obra nos dice:
".. Y el problema,
Trazar una recta por un punto dado que divida un triángulo dado en dos
partes cuyas áreas estén según una razón dada,
puede resolverse reduciéndolo a la siguiente construcción:
Trazar desde un punto dado la tangente a una hipérbola de la que se conocen
las asíntotas y una tangente.
Se deja como ejercicio para el estudiante."
Trazar una recta por un punto dado que divida un triángulo dado
en dos partes cuyas áreas estén según una razón
dada.
|
 |
|
Propuesto por Jose María Pedret.
|
Solución de Francisco
Javier García Capitán
Análisis con coordenadas baricéntricas
Haremos el análisis del problema usando las coordenadas baricéntricas.
Seguimos el esquema trazado por Paul
Yiu en su Introduction to the Gometry of the Triangle (en adelante
Introducción), en la sección 11.4.2, donde se trata el
caso particular de que las dos áreas sean iguales. Por conveniencia,
en lugar de comparar el área de las dos partes resultantes de la división,
compararemos el área del triángulo resultante con el área
del triángulo de partida, supondemos que las dos áreas están
en la razón m:n.
Sea Y un punto de la recta AC. Existe un único punto Z
sobre la recta AB tal que el área (con signo) del triángulo
AZY es la fracción m:n del área del triángulo
ABC. Hallemos este punto Z:
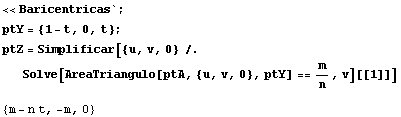
Entonces la ecuación de la recta YZ es

Según podemos ver en el apartado 11.4 de la Introducción,
la envolvente de la familia paramétrica de rectas
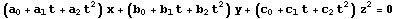
es la cónica de ecuación
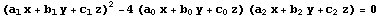
siempre que la matriz
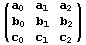
tenga determinante no nulo. En nuestro caso,
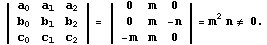
Por tanto la envolvente será:
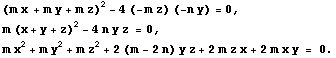
Introduciendo la ecuación de la cónica podemos hallar fácilmente
su centro y su discriminante:

Vemos que se trata de una hipérbola, ya que su discriminante
es positivo, y que el centro es el vértice A. Además,
los puntos (1 : -1 : 0) y {1 : 0 : -1)
cumplen evidentemente la ecuación
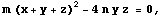
por lo que pertenecen a la hipérbola.
Estos puntos, cuyas coordenadas suman cero, son los puntos del infinito de
las rectas AB y AC, respectivamente.
Deducimos que estas rectas son las asíntotas de la hipérbola,
y además los ejes de la hipérbola serán las bisectrices
exterior e interior del ángulo A. Esto permite hallar los vértices
de la hipérbola. Para ello, hallamos los puntos de intersección
de la cónica con la bisectriz interior, resultando dos puntos. Si lo
intentamos con la bisectriz exterior obtendremos puntos imaginarios.
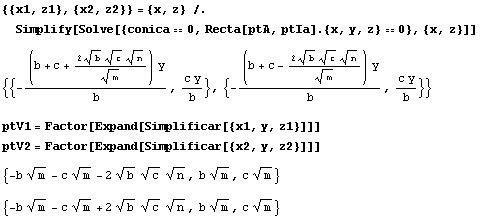
Desgraciadamente, las fórmulas obtenidas para los vértices no
son sencillas, pero podemos usar la fórmula del cuadrado de la distancia
para hallar la distancia entre ellos:
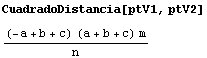
Esto quiere decir que la distancia desde el centro A a cada uno de los
vértices V1 y V2 de la hipérbola será

Construcción con Cabri
La fórmula que acabamos de encontrar permite la construcción
con regla y compás de los vértices de la hipérbola. A partir
de ahí podemos encontrar los focos y algunos puntos de la hipérbola,
lo que nos permitrá trazar dicha hipérbola con Cabri.
|
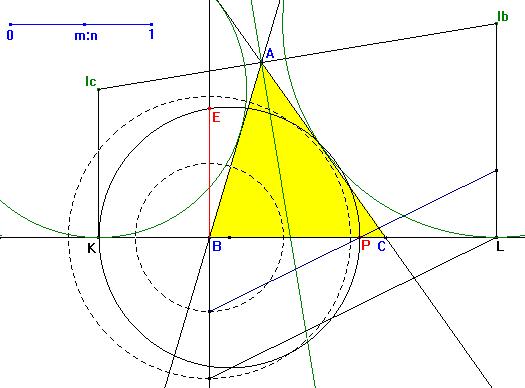 La figura
muestra el triángulo ABC y las circunferencias exinscrits
(Ib) e (Ic), que tocan a la recta
BC en L y K, respectivamente. Sabemos que BK
= s-a y BL = s.
Usaremos que el semiperímetro s del triángulo ABC
y la longitud s-a son fáciles
de identificar en un triángulo ABC. En la figura también
hemos colocado un deslizador que nos permitirá introducir
la proporción m:n. Esta proporción variará
de 0 a 1. La figura
muestra el triángulo ABC y las circunferencias exinscrits
(Ib) e (Ic), que tocan a la recta
BC en L y K, respectivamente. Sabemos que BK
= s-a y BL = s.
Usaremos que el semiperímetro s del triángulo ABC
y la longitud s-a son fáciles
de identificar en un triángulo ABC. En la figura también
hemos colocado un deslizador que nos permitirá introducir
la proporción m:n. Esta proporción variará
de 0 a 1.
Lo primero que hacemos es construir un punto P en BL tal
que BP:BL = m:n.
Ahora bastará hallar la media geométrica de los segmentos
BK y BP, es decir un segmento BE tal que BE2
= BP·BK. Para ello hallamos una circunferencia con
diámetro KP y hallamos el punto E en la intersección
de dicha circunferencia con la perpendicular a KP por B.
|
|
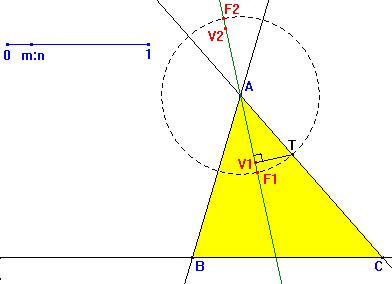 Una vez
conocida la distancia AV1 = AV2 = BE, llemamos dicha
distancia sobre la bisectriz interior del ángulo A y obtenemos
los vértices V1 y V2. Una vez
conocida la distancia AV1 = AV2 = BE, llemamos dicha
distancia sobre la bisectriz interior del ángulo A y obtenemos
los vértices V1 y V2.
A partir de aquí podemos obtener los focos trazando una perpendicular
a la bisectriz (eje principal) por uno de los vértices, que se
encontrará con uno de los lados en un punto T. La circunferencia
con centro A y radio T corta a la bisectriz en los focos
F1 y F2 de la hipérbola.
Teniendo los focos de la hipérbola basta aplicar el método
estándar para hallar algunos puntos de la curva que nos permitan
usar la herramienta de Cabri para hallar trazar la cónica que pasa
por cinco puntos.
|
|
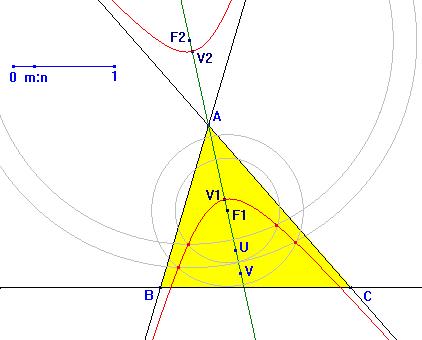 Esta construcción
de puntos de la hipérbola se hace tomando puntos arbitrarios U,
V, ... sobre el eje focal (la bisectriz en nuestro caso) que no
estén en el segmento limitado por los focos. Ahora, con el punto
U tomamos los radios UV1 y UV2
y trazamos las circunferencias con centros F1 y F2
respectivamente. Los puntos de intersección de estas circunferencias
pertenecerán a la hipérbola. Esta construcción
de puntos de la hipérbola se hace tomando puntos arbitrarios U,
V, ... sobre el eje focal (la bisectriz en nuestro caso) que no
estén en el segmento limitado por los focos. Ahora, con el punto
U tomamos los radios UV1 y UV2
y trazamos las circunferencias con centros F1 y F2
respectivamente. Los puntos de intersección de estas circunferencias
pertenecerán a la hipérbola.
Haciendo la construcción para dos puntos obtendremos cuatro puntos
de la hipérbola, que añadidos a los dos vértices
que conocemos hacen SEIS puntos, uno más de los que necesitamos.
|
|
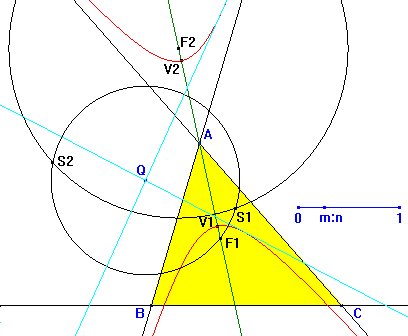 Una vez
construida la hipérbola, dado un punto cualquiera P, lo
único que tenemos que hacer es trazar a dicha hipérbola
la tangente desde Q. Una vez
construida la hipérbola, dado un punto cualquiera P, lo
único que tenemos que hacer es trazar a dicha hipérbola
la tangente desde Q.
Para ello recurrimos a la recta que podemos encontrar en Trazado Geométrico,
de M. González Monsalve y J. Palencia Cortés, pág.
253:
- Trazamos una circunferencia con centro F_2 y radio V_1V_2
y otra circunferencia con centro Q y radio F_1 y radio
QF_1.
- Hallamos los puntos de intersección S_1 y S_2
de estas dos circunferencias.
- Las mediatrices de los segmentos F_1S_1 y F_1S_2
las tangentes a la hipérbola desde Q.
|
Discusión de la solución obtenida
|
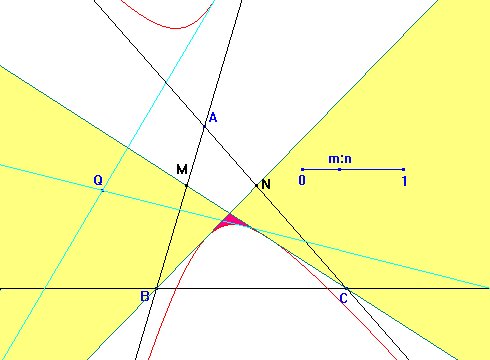 La discusión
es parecida a la vista para el problema 137. La discusión
es parecida a la vista para el problema 137.
Como vemos en la figura, las rectas tangentes desde B y C
a la hipérbola dividen al plano en cuatro regiones.
Cuando el punto Q pertenezca a las regiones sombreadas en amarillo,
exactamente una de las rectas tangentes desde Q dará lugar
a una solución del problema.
Si el punto Q pertenece a la región coloreada en morado,
cada una de las dos rectas tangentes dará lugar a una solución.
Finalmente si el punto Q pertenece a alguna de las regiones que
han quedado en blanco ninguna de las rectas tangentes dará lugar
a una solución.
|
|
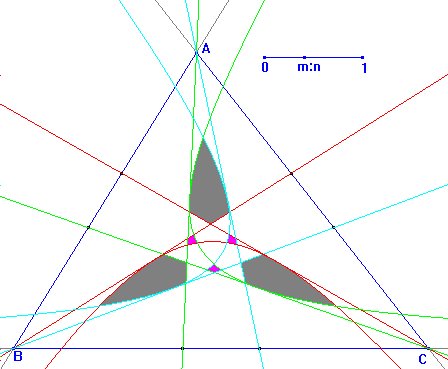 Para finalizar
digamos que si el punto Q queda fuera de las regiones con solución,
puede intentarse la construcción usando la hipérbola correspondiente
a otro de los vértices. Para finalizar
digamos que si el punto Q queda fuera de las regiones con solución,
puede intentarse la construcción usando la hipérbola correspondiente
a otro de los vértices.
Sin embargo, como muestra la figura, puede haber regiones, como las coloreadas
en gris en la figura, en las que no se obtengan soluciones con ninguna
de las tres hipérbolas, careciendo el problema de solución.
Observamos que también hay regiones (las tres marcadas en rosa)
formadas por puntos con dos soluciones para dos de las hipérbolas,
por lo que en ese caso el problema tendría cuatro soluciones.
|

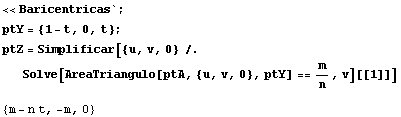
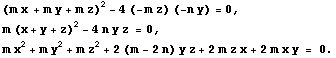

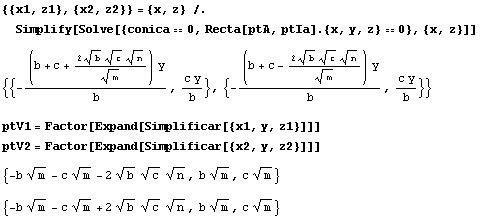
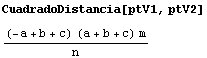
 La figura
muestra el triángulo ABC y las circunferencias exinscrits
(Ib) e (Ic), que tocan a la recta
BC en L y K, respectivamente. Sabemos que BK
= s-a y BL = s.
Usaremos que el semiperímetro s del triángulo ABC
y la longitud s-a son fáciles
de identificar en un triángulo ABC. En la figura también
hemos colocado un deslizador que nos permitirá introducir
la proporción m:n. Esta proporción variará
de 0 a 1.
La figura
muestra el triángulo ABC y las circunferencias exinscrits
(Ib) e (Ic), que tocan a la recta
BC en L y K, respectivamente. Sabemos que BK
= s-a y BL = s.
Usaremos que el semiperímetro s del triángulo ABC
y la longitud s-a son fáciles
de identificar en un triángulo ABC. En la figura también
hemos colocado un deslizador que nos permitirá introducir
la proporción m:n. Esta proporción variará
de 0 a 1.  Una vez
conocida la distancia AV1 = AV2 = BE, llemamos dicha
distancia sobre la bisectriz interior del ángulo A y obtenemos
los vértices V1 y V2.
Una vez
conocida la distancia AV1 = AV2 = BE, llemamos dicha
distancia sobre la bisectriz interior del ángulo A y obtenemos
los vértices V1 y V2.  Esta construcción
de puntos de la hipérbola se hace tomando puntos arbitrarios U,
V, ... sobre el eje focal (la bisectriz en nuestro caso) que no
estén en el segmento limitado por los focos. Ahora, con el punto
U tomamos los radios UV1 y UV2
y trazamos las circunferencias con centros F1 y F2
respectivamente. Los puntos de intersección de estas circunferencias
pertenecerán a la hipérbola.
Esta construcción
de puntos de la hipérbola se hace tomando puntos arbitrarios U,
V, ... sobre el eje focal (la bisectriz en nuestro caso) que no
estén en el segmento limitado por los focos. Ahora, con el punto
U tomamos los radios UV1 y UV2
y trazamos las circunferencias con centros F1 y F2
respectivamente. Los puntos de intersección de estas circunferencias
pertenecerán a la hipérbola.  Una vez
construida la hipérbola, dado un punto cualquiera P, lo
único que tenemos que hacer es trazar a dicha hipérbola
la tangente desde Q.
Una vez
construida la hipérbola, dado un punto cualquiera P, lo
único que tenemos que hacer es trazar a dicha hipérbola
la tangente desde Q. La discusión
es parecida a la vista para el problema 137.
La discusión
es parecida a la vista para el problema 137.  Para finalizar
digamos que si el punto Q queda fuera de las regiones con solución,
puede intentarse la construcción usando la hipérbola correspondiente
a otro de los vértices.
Para finalizar
digamos que si el punto Q queda fuera de las regiones con solución,
puede intentarse la construcción usando la hipérbola correspondiente
a otro de los vértices.