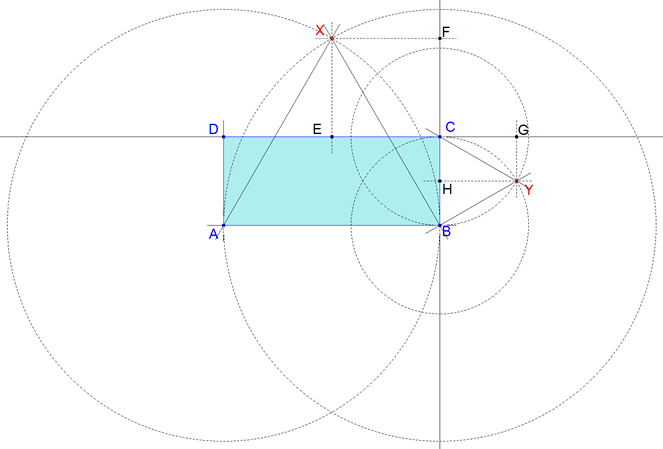
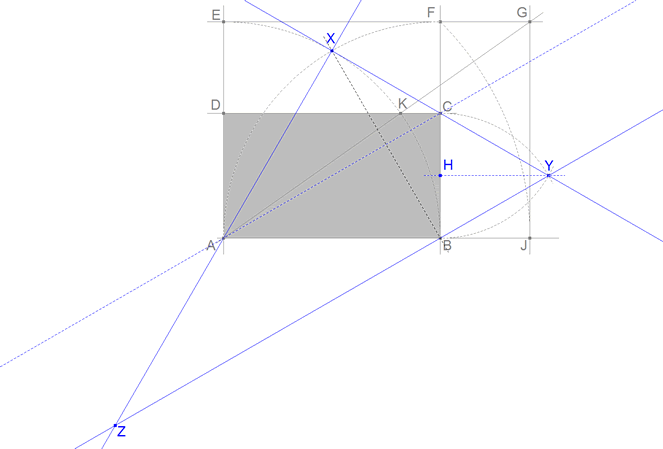
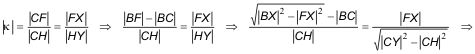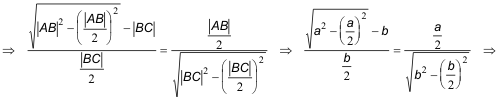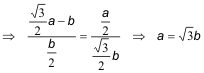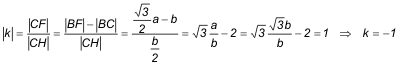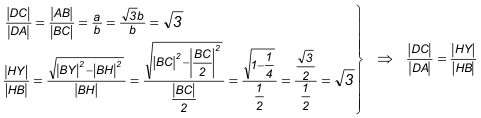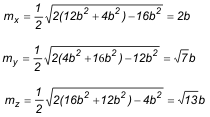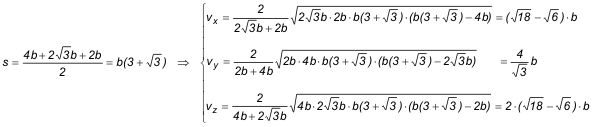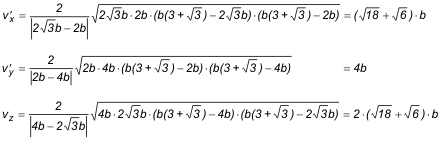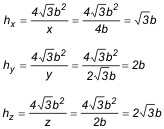Problema 304.
Dado el rectángulo ABCD, con a=AB (base) y b=BC (altura), a>b, desde la base AB se construye internamente el triángulo equilátero ABX, y desde la altura, b=BC, se construye exteriormente un triángulo equilátero BCY. Las rectas AX y BY se cortan en Z. Se pide:

a) Hallar la relación entre la base y la altura del rectángulo para que los puntos X, C e Y, estén alineados.

b) Caracterizar y calcular en este caso todos los elementos significativos: lados, ángulos, medianas, bisectrices interiores y exteriores, radio inscrito y radio circunscrito del triángulo XYZ.

Romero, JB. (2006). Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de marzo de 2006)

APARTADO (a)

CONDICIONES DEL ENUNCIADO

figura 1

Si X, C, Y estuvieran alineados, los triángulos CFX y CHY serían homotéticos con centro de homotecia en C. Ya que tendrían dos lados paralelos y el tercero, por C, en prolongación.

Expresando la razón de la homotecia

que es la condición buscada. Además

Y como C es el centro de homotecia y la razón es κ = -1

deducimos que

¡¡¡ C ES EL PUNTO MEDIO DE XY !!!

COMPROBACIÓN CON CABRI II

figura 2

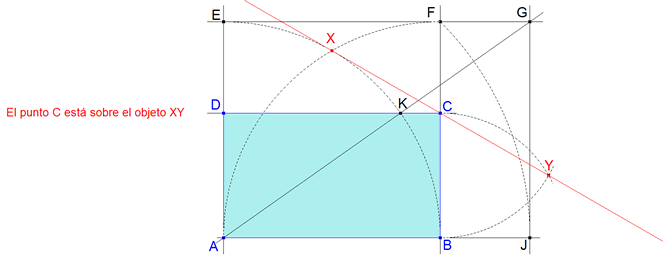
1 Trazamos la recta AB y una perpendicular por A.
2 Con centro en A arco de radio AB que corta en E a la perpendicular anterior.
3 La paralela por E a AB y la paralela por B a AE se cortan en F.
4 Con centro en A arco de radio AF que corta a AB en J.
5 Por J perpendicular a AB que corta a EF en G.
6 La recta EF corta al arco BE en K.
7 Por K, paralela a AB que corta a AE en D y a BF en C.

Hecha la construcción vemos que:

APARTADO (b)

figura 3

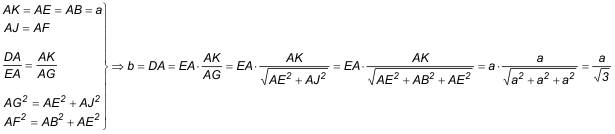
ÁNGULOS

Como los triángulos construídos son equiláteros, sus lados serán respectivamente a y b y sus ángulos serán todos

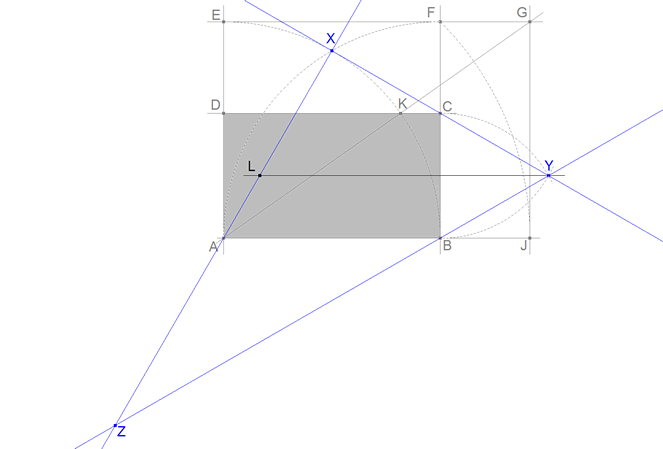
Para ayudarnos, trazamos por Y una paralela a AB que corta a AX en L

lo que nos lleva a

Lo que nos dice que

XYZ ES RECTÁNGULO EN X,

y entonces

LADOS

figura 4

Gracias a que C es el punto medio de XY

Comparemos ahora los triángulos ADC y BHY

Lo que significa que los triángulos ADC y BHY son semejantes; pero los lados AD y DC son respectivamente paralelos a BH y HY, entonces los terceros lados AC y BY son paralelos; lo que nos lleva a que

¡¡¡ AC y ZY SON PARALELAS !!!

Por lo que podemos escribir

Y como sabemos que XYZ es rectángulo en X

MEDIANAS

A partir de la figura, y aprovechando que el triángulo es rectángulo, podríamos determinar las medianas; pero haremos el cálculo a partir de las fórmulas generales siguientes