Problema 304

Donat el rectangle ABCD amb (base) i altura i des de la base es construeix internament el triangle equilàter i des de l’altura es construeix exteriorment un triangle equilàter . Les rectes AX i BY es tallen en el punt Z. Es demana:

a) Determinar la relació entre la base i l’altura del rectangle a fi que els punts X, C Y estiguen alineats.

b) Caracteritzeu i calculeu en aquest cas tots els elements significatius: costats, angles, mitjanes, bisectrius interiors i exteriors, radi inscrit i radi circumscrit del triangle .

Romero, JB. (2006). Comunicación personal

SolucióSolución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València) (16 de marzo de 2006) (en valenciano) :

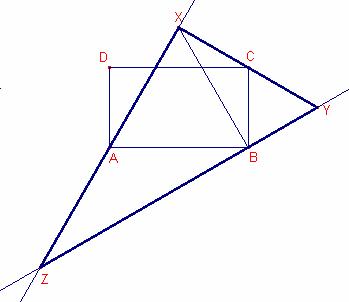
a)

A fi que els punts X, C i Y estiguen alineats l’angle ha de ser pla.

per ser el triangle equilàter.

per ser ABCD un rectangle.

Aleshores per estar alineats l’angle

En aquesta cas .

Per tant el triangle és isòsceles

i el triangle és rectangle. , .

Aplicant el teorema de Pitàgores al triangle rectangle :

Aleshores, .

b)

Aleshores, el triangle és rectangle.

, .

, .

Aplicant el teorema de Pitàgores al triangle :

.

Calculem les mitjanes:

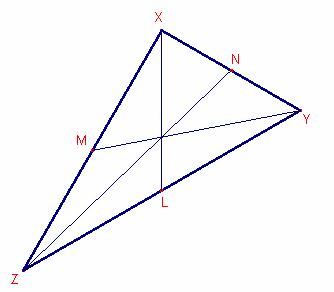
Siguen les mitjanes del triangle .

La mitjana sobre la hipotenusa d’un triangle rectangle mesura la meitat que la hipotenusa, aleshores,

.

Aplicant el teorema de Pitàgores al triangle rectangle :

.

Aplicant el teorema de Pitàgores al triangle rectangle :

.

Calculem les bisectrius interiors:

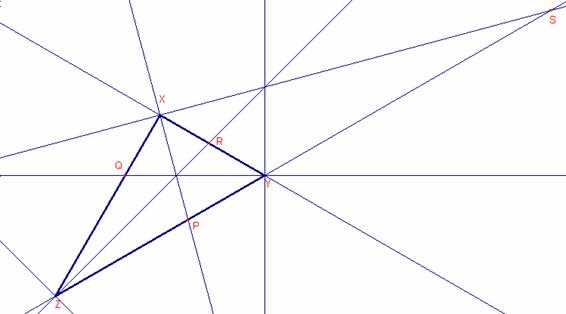
Siguen les bisectrius interiors al triangle .

Aplicant el teorema dels sinus al triangle :

,

Aplicant raons trigonomètriques al triangle rectangle

.

Aplicant raons trigonomètriques al triangle rectangle

.

Calculem les bisectrius exteriors:

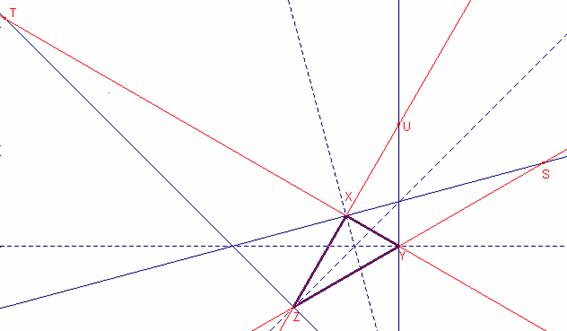
Siguen les bisectrius exteriors al triangle .

, .

Aplicant el teorema dels sinus al triangle :

,

Aplicant raons trigonomètriques al triangle rectangle

.

Aplicant raons trigonomètriques al triangle rectangle

.

Calculem el radi de la circumferència inscrita i la circumscrita.

En un triangle rectangle el radi R de la circumferència circumscrita mesura la meitat de la hipotenusa.

.

En un triangle rectangle el radi r de la circumferència inscrita mesura el semiperímetre menys la hipotenusa.

.