Problema 304.

Dado el rectángulo ABCD, con a =AB (base) y b = BC ( la altura), y a>b desde la base AB se construye internamente el triángulo equilátero ABX, y desde la altura, b= BC, se construye exteriormente un triángulo equilátero BCY. Las rectas AX y BY se cortan en Z.

Se pide :

a) Hallar la relación entre la base y la altura del rectángulo para que los puntos X, C e Y, estén alineados.

b) Caracterizar y calcular en este caso todos los elementos significativos: lados, ángulos, medianas, bisectrices interiores y exteriores, radio inscrito y radio circunscrito del triángulo XYZ.

Romero, JB. (2006). Comunicación personal

SoluciónSolución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València) (16 de marzo de 2006)

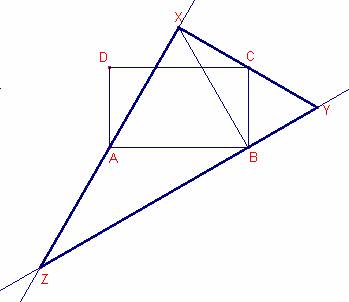
a)

Para que los puntos X, C y Y estén alineados el ángulo tiene que ser llano.

por ser el triángulo equilátero.

por ser ABCD un rectángulo.

Entonces por estar alineados el ángulo

En este caso .

Por tanto el triángulo es isósceles

y el triángulo es rectángulo. , .

Aplicando el teorema de Pitágoras al triángulo rectángulo :

Entonces, .

b)

Entonces, el triángulo es rectángulo.

, .

, .

Aplicando el teorema de Pitágoras al triángulo :

.

Calculemos las medianas:

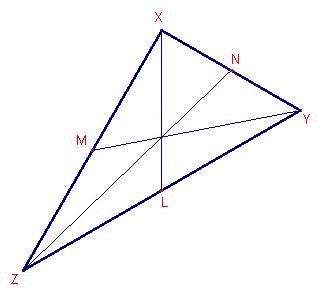
Sean las medianas del triángulo .

La mediana sobre la hipotenusa de un triángulo rectángulo mide la mitad que la hipotenusa, entonces,

.

Aplicando el teorema de Pitágoras al triángulo rectángulo :

.

Aplicando el teorema de Pitágoras al triángulo rectángulo :

.

Calculemos las bisectrices interiores:

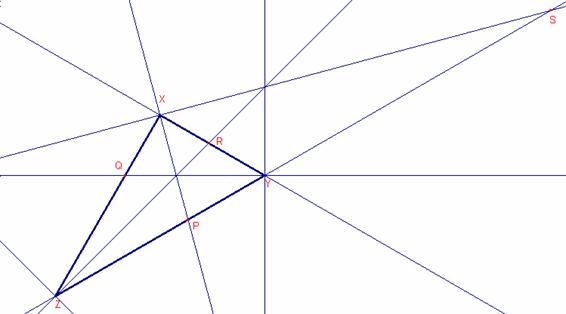
Sean les bisectrices interiores del triángulo .

Aplicando el teorema de los senos al triángulo :

,

Aplicando razones trigonométricas al triángulo rectángulo

.

Aplicando razones trigonométricas al triángulo rectángulo

.

Calculemos las bisectrices exteriores:

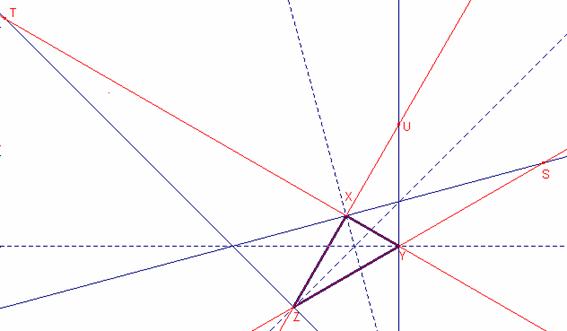
Sean las bisectrices exteriores del triángulo .

, .

Aplicando el teorema de los senos al triángulo :

,

Aplicando razones trigonométricas al triángulo rectángulo

.

Aplicando razones trigonométricas al triángulo rectángulo

.

Calculemos el radio de la circunferencia inscrita y la circunscrita.

En un triángulo rectángulo el radio R de la circunferencia circunscrita mide la mitad de la hipotenusa.

.

En un triángulo rectángulo el radio r de la circunferencia inscrita mide el semiperímetro menos la hipotenusa.

.