Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

De investigación

Problema 305.- Sea el triángulo ABC y dada la ceviana arbitraria AA' donde A´, varía sobre el lado BC. Construimos los triángulos rectángulos en el vértice A, que denotamos por ACB* y ABC* donde B* y C* son los puntos más próximos a B y C, y situados tal vez en la prolongación del lado BC. Por A'  trazamos la recta perpendicular a AA', y los puntos de corte de ésta, con AC, AC*, AB, AB* los designamos por B(A), N(A),C(A), M(A), respectivamente. Y, con ellos, construimos los cuadriláteros P(A) = C(A)BB*M(A) y  Q(A) =CB(A)N(A)C*.

 a)  Si  X(A) e Y(A) son los puntos que se obtienen como intersección de las diagonales de los cuadriláteros P(A) y Q(A), respectivamente, entonces X(A), A', Y(A) están alineados.

b) Lugares geométricos descritos  por los puntos X(A), e Y(A), cuando A'  varía sobre la recta que contiene al lado BC, respectivamente.

Romero, J.B. (2006): Comunicación personal

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

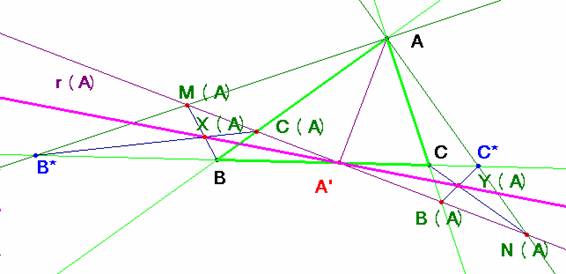
a) Dado A’, construyo la recta r(A) como la perpendicular a AA’ por éste último. Tomando r=BC defino, con el punto A como vértice, una proyección entre estas rectas.

Se corresponden los puntos (M(A), C(A), A’, B(A), N(A) ) de r(A) con los puntos de r (B*, B, A’, C, C*).

Una proyección es una homografía y los puntos X(A), A’ e Y(A) pertenecen al eje proyectivo de la misma: están alineados.

b) Los puntos B*, C* dependen exclusivamente del triángulo dado para cualquier ceviana AA’ que se tome. Como X(A) se expresa como intersección de dos rectas por B y B* estamos inclinados a pensar si este punto describirá al variar A’, una cónica, pero no es así. La imagen de una recta que pase por B corta a la recta AB* en un punto, llamésmolo B”. El punto A’ del que procede se obtendría por intersección de la circunferencia de diámetro B”A con el lado BC. Ya aparece un primer inconveniente: habría dos puntos de corte y otro más: podría no haber ninguno. Así pues no siempre se podría determinar una proyectividad entre las rectas de un haz de vértice B con las de otro haz de vértice B*. En conclusión, sin saber cuál es el lugar geométrico descrito por X(A), sí podemos decir que no es una cónica.

Conclusiones análogas se establecen para el otro punto Y(A).