Para el aula.

Propuesto por Juan Carlos Salazar, profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz)

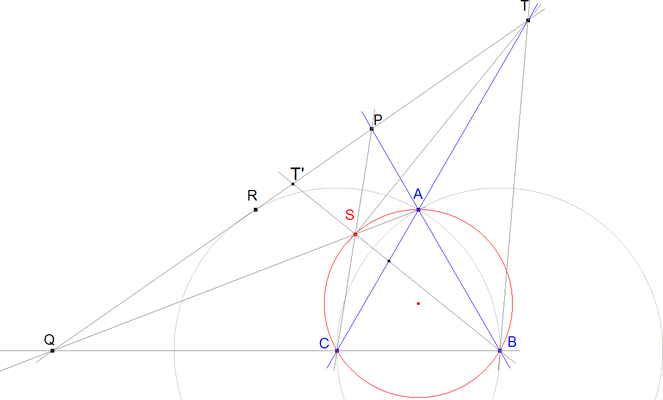
Problema 306

Sea el triángulo equilátero ABC, por el punto R simétrico de B con respecto a AC se traza una recta que corta a las prolongaciones de BA y BC en P y Q respectivamente. Además si S es el punto de corte de AQ y PC, y T es el punto de corte de AC y PQ. Demostrar que: SB = SA + SC y <BST = 90º.

Salazar, J. C. (2006): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (02 de abril de 2006)

figura 1

Como la recta PQ rota en torno a R, induce una homografía h:AB→BC tal que h(P)=Q=PR∩BC ∀ P∈AB.

En estas condiciones la biyección entre haces de rectas h*:C*→A* tal que h*(CP)=AQ es una homografía y por el Teorema de Chasles-Steiner, el lugar geométrico de S=CP∩AQ=CP∩h*(CP) es una cónica que pasa por C y A. Si P=B nos dice que la cónica pasa por B. Por el mismo teorema h*(CA)=AA que es la tangente en A; pero esa tangente es paralela a BC y h*^-1(AC)=CC que es la tangente en C y paralela a AB. Por lo tanto:

Si la cónica pasa por A, B, C, la tangente en A es paralela a BC y la tangente en C es paralela a AB, esa cónica es el CÍRCULO CIRCUNSCRITO a ABC.

Si aplicamos el Teorema de Ptolomeo al cuadrilátero ABCS inscrito en el círculo anterior, tenemos que la suma de productos de los lados opuestos es igual al producto de diagonales, que en nuestro caso queda

SAxBC+SCxAB=SBxCA

pero en el triángulo equilátero AB=BC=CA, lo que nos proporciona el resultado buscado.

SA+SC=SB

Si seguimos observando la figura ∠CSA=⅔π y ∠BSA=⅓π; entonces BST' es la bisectriz de ∠CSA y por tanto de ∠PSQ; pero por el cuadrilátero PQCA, T' es el conjugado armónico de T, recordando que las bisectrices cortan al lado opuesto en puntos conjugados armónicos, ST será la bisectriz de ∠PSA y por lo tanto bisectriz exterior de ∠CSA de lo que podemos concluir que BS y TS son perpendiculares, es decir

∠BST=½π.