Problema 306

Sea el triángulo equilátero ABC, por el punto R simétrico de B con respecto a AC se traza una
recta que corta a las prolongaciones de BA y BC en P y Q respectivamente. Además si S es  el punto de corte
de AQ y PC, y T es el punto de corte de AC y PQ. Demostrar que: SB = SA + SC y <BST = 90º.

Salazar, J. C. (2006): Comunicación personal.

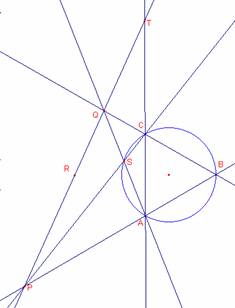
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València) :

Sea el lado del triángulo equilátero.

Sea ,

Los triángulos , son semejantes, entonces:

.

Sea , . Veamos que .

Aplicando el teorema de los senos al triángulo :

(1)

Aplicando el teorema de los senos al triángulo :

(2)

Multiplicando las expresiones (1) (2)

Teniendo en cuenta que y simplificando:

.

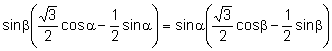
Entonces, .

Entonces,

Por tanto el cuadrilátero ABCS es inscriptible ya que los ángulos opuestos suman 180º.

Aplicando el teorema de Tolomeo:

Simplificando:

.