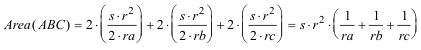201. La suma de los inversos de los radios de los círculos ex-inscritos de un triángulo es igual al inverso del radio del círculo inscrito, y la raíz cuadrada del producto de los cuatro radios es igual al área del círculo (sic) [Es un “despiste”, se trata del área del triángulo N. del D.].

Severi, F. (1952) : Elementos de geometría II, con 144 figuras, traducción de la segunda edición italiana por el profesor T. Martín Escobar, de la Escuela Industrial de Gijón. Tercera reimpresión. Editorial Labor, Barcelona. Talleres Gráficos Ibero-Americanos S.A. Reproducción offset. (pág 201)

Del prólogo:

…Tener a la vista el origen histórico y buscar el fundamento psicológico de cada teoría y sobre todo las nociones de sentido común de donde ésta nace para encontrar la vía didácticamente más oportuna.

Descubierta la vía maestra, es necesario comenzar de nuevo y desbrozar los senderos que en ella desembocan de las dificultades demasiado graves para los inexpertos, de modo que el alumno pueda recorrerlos siguiéndonos, sin excesivo esfuerzo, en el proceso constructivo.

Hacer que todo esto se encuentre liso y llano, no conviene. Desvanece el deseo juvenil de la conquista, y la teoría, ya demasiado afinada, aparece lejana de la vida e interesa poco…

 

También daremos por sabida la fórmula de Herón para expresar el área del triángulo en función de los lados.

 

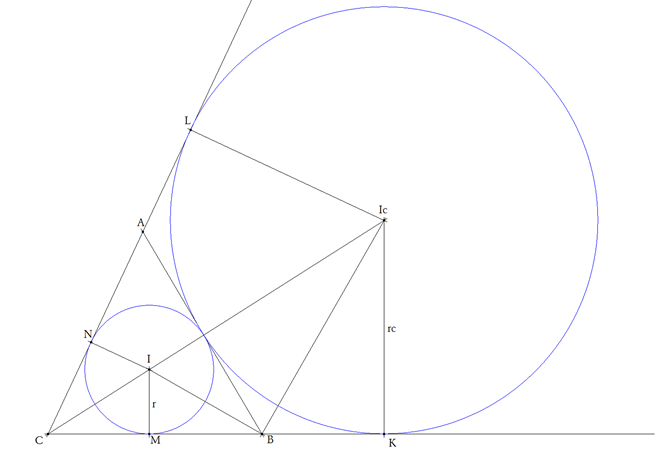
También es claro (ver figura) que podemos tomar al círculo inscrito I y al ex-inscrito Ic como homotéticos con centro de homotecia en C y razón de homotecia la razón de radios. Consideraciones parecidas podemos hacer con Ia e Ib.

Si nos fijamos en el círculo inscrito I y en el ex-inscrito Ic, el triángulo IBC tiene por área

Teniendo en cuenta a los otros círculos ex-inscritos las áreas de sus triángulos tendrán expresiones análogas y por lo tanto podremos expresar el área del triángulo ABC como suma de las áreas de los tres triángulos análogos a IBC

Por otra parte, comparando los triángulos IMC e IcKC teniendo en cuenta que son homotéticos

Considerando también a los otros círculos ex-inscritos podemos expresar