Problema 308

Aplicacions de l’àlgebra a la geometria

201. La suma dels inversos dels radis dels cercles exinscrits d’un triangle és igual a l’invers del radi del cercle inscrit, i l’arrel quadrada del producte dels quatre radis és igual a l’àrea del triangle.

Severi, F. (1952) : Elementos de geometría II, con 144 figuras, traducción de la segunda edición italiana por el profesor T. Martín Escobar, de la Escuela Industrial de Gijón. Tercera reimpresión. Editorial Labor, Barcelona. Talleres Gráficos Ibero-Americanos S.A. Reproducción offset. (pág 201)

Propietat: Proporció entre els radis de les circumferències inscrites i exinscrites.

Siga el triangle .

Siguen r i els radis de les circumferències inscrita i exinscrita, respectivament.

Aleshores, on p és el semiperímetre del triangle .

Demostració:

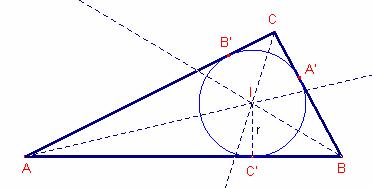
Siguen els punts A’, B’, C’ els punts de tangència de la circumferència inscrita al triangle amb els costats.

.

Aleshores, .

.

Per tant .

Anàlogament, .

Siga la circumferència exinscrita de centre i radi .

Siguen A”, B”, C” els punts de tangència de la circumferència inscrita al triangle amb les prolongacions dels costats.

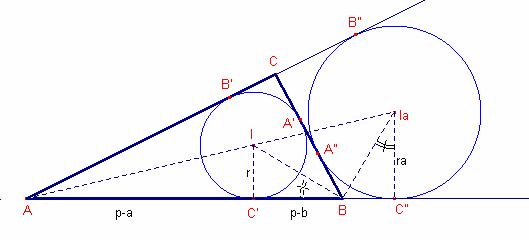
Calculem i .

.

Aleshores;

Sumant les expressions:

, aleshores, .

Per tant, .

Els triangle , són semblants, aleshores, .

Anàlogament, , .

Fórmula d’Heró. L’àrea d’un triangle és:

.

O bé: .

Fórmula de l’àrea en funció del radi de la circumferència inscrita. L’àrea d’un triangle és:

on p és el semiperímetre .

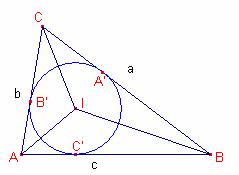
Siga I l’incentre del triangle . Siga r el radi de la circumferència inscrita a . Siguen A’, B’, C’, els punts de tangència de la circumferència inscrita i el triangle .

Podem notar que .

L’àrea del triangle és igual a la suma de les àrees dels triangles , ,

.

Nota 1: Fórmula per a calcular el radi de la circumferència inscrita en funció dels costats.

.

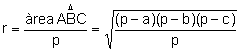Nota 2: A partir de la proporció entre els radis de les circumferències inscrita i exinscrites tenim les fórmules dels radis de les exinscrites en funció dels costats:

, ,

En qualsevol triangle la relació dels radis de la circumferència inscrita, i de les exinscrites és la següent:

.

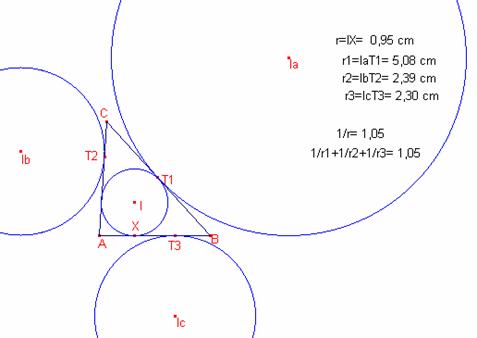
Demostració

A partir de la proporció entre els radis de la circumferència inscrita i les exinscrites obtenim:

, , , on .

.

Dividint l’expressió per r:

.

Nota: Una altra fórmula de radis: .

Siga el triangle .

Siguen r el radi de la circumferència inscrita i r_a r_b r_c els radis de les circumferències exinscrites.

Aleshores: L’àrea del triangle és .

Demostració:

A partir de la proporció entre els radis de les circumferències inscrita i exinscrites obtenim les fórmules dels radis de les exinscrites en funció dels costats:

, , , on

El radi de la circumferència inscrita en funció dels costats és: .

.

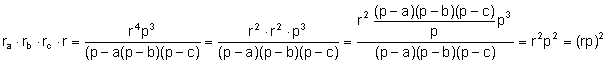
Aleshores, .