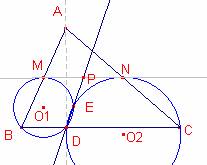
Problema 310
Siga 
l’altura al costat 
del triangle 
. Siga M i N els punts mig dels costats 
i 
, respectivament. Siga E el segon punt d’interseccció de les circumferències circumscrites als triangles 
i 
. Proveu que la recta DE passa pel punt mig del segment 
.
X Olimpíada Matemática Rioplatense
San Isidro, 13 de Diciembre de 2001
Nivel I – Segundo Día
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València) (en valenciano):
Considerem els vèrtex del triangle amb les següents coordenades cartesianes: 
.
Les coordenades del peu de l’altura són 
Les coordenades del punt mig M del segment i N punt mig del segment són: 
, 
.
Les coordenades del punt mig P del segment són 
Determinem el centre 
de la circumferència circumscrita al triangle :
La recta mediatriu del segment 
té equació 
.
La recta mediatriu del segment 
té equació 
.
La intersecció de les rectes 
, 
és el centre de la circumferència circumscrita al triangle . Les seues coordenades són: 
Determinem el centre 
de la circumferència circumscrita al triangle :
La recta mediatriu del segment 
té equació 
.
La recta mediatriu del segment 
té equació 
.
La intersecció de les rectes 
, 
és el centre de la circumferència circumscrita al triangle . Les seues coordenades són: 
.
Siga E el punt d’intersecció d’ambdues circumferències (distint de D)
La recta que passa pels punts D, E és perpendicular al segment 
.
La recta que passa per D, E és la recta que passa per D i té per vector director 
.
Simplificant el vector director és 
).
L’equació de la recta que passa pels punts D, E té equació: 
El punt és de la recta r ja que satisfà la seua equació:
.
Amb Cabri:
Figura barroso310.fig
Applet created on 1/05/06 by Ricard Peiró with CabriJava