Problema 310
- 0.1 Sea AD la altura relativa al lado BC del triángulo acutángulo ABC. M y N son los puntos medios de los lados AB y AC, respectivamente. Sea E el segundo punto de intersección de las circunferencias circunscritas a los triángulos BDM y CDN.
Muestra que la recta DE pasa por el punto medio de MN.
X Olimpíada Matemática Rioplatense
San Isidro, 13 de Diciembre de 2001
Nivel I – Segundo Día
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València) (en español):
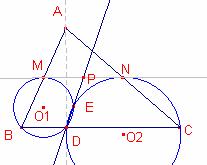
Consideremos los vértices del triángulo 
con las siguientes coordenadas cartesianas: 
.
Las coordenadas del pie de la altura 
son 
Las coordenadas del punto medio M del segmento 
y N punto medio del segmento son: 
, 
.
Las coordenadas del punto medio P del segmento 
son 
Determinemos el centro 
de la circunferencia circunscrita al triángulo 
:
La recta mediatriz del segmento 
tiene ecuación 
.
La recta mediatriz del segmento 
tiene ecuación 
.
La intersección de las rectas 
, 
es el centro de la circunferencia circunscrita al triángulo . Sus coordenadas son: 
Determinemos el centro 
de la circunferencia circunscrita al triángulo 
:
La recta mediatriz del segmento 
tiene ecuación 
.
La recta mediatriz del segmento 
tiene ecuación 
.
La intersección de las rectas 
, 
es el centro de la circunferencia circunscrita al triángulo . Sus coordenadas son: 
.
Sea E el punto de intersección de ambas circunferencias (distinto de D)
La recta que pasa por los puntos D, E es perpendicular al segmento 
.
La recta que pasa por D, E es la recta que pasa por D y tiene por vector director 
.
Simplificando el vector director es 
).
La ecuación de la recta que pasa por los puntos D, E tiene ecuación: 
El punto es de la recta r ya que satisface su ecuación:
.
Con Cabri:
Figura barroso310.fig
Applet created on 1/05/06 by Ricard Peiró with CabriJava