Problema para el aula

Problema 310

• 0.1 Sea AD la altura relativa al lado BC del triángulo acutángulo ABC. M y N son los puntos medios de los lados AB y AC, respectivamente. Sea E el segundo punto de intersección de las circunferencias circunscritas a los triángulos BDM y CDN.

Muestra que la recta DE pasa por el punto medio de MN.

X Olimpíada Matemática Rioplatense

San Isidro, 13 de Diciembre de 2001

Nivel I – Segundo Día

http://www.oma.org.ar/enunciados/omr10.doc

Solución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú

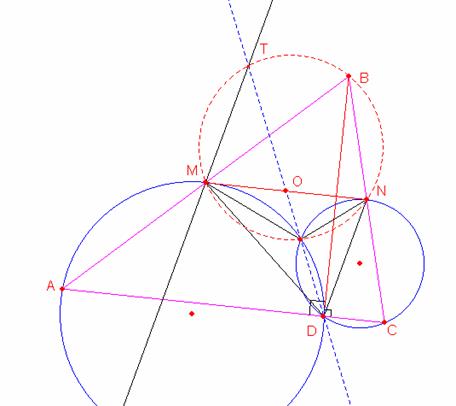
Sabemos que:

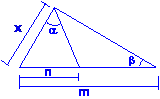
Se cumple que β = α

Además en todo triángulo isósceles toda paralela a las base es tangente a la circunferencia circunscrita al triángulo.

Sea la grafica con los datos indicados

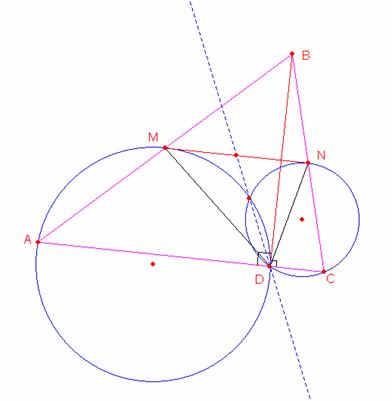
Por propiedad sabemos que el cuadrilátero MBNF es inscriptible (puntos de Miquel)

Primero demostraremos que las rectas que pasan por los punto M, T y D, N son paralelas

Del gráfico observamos que

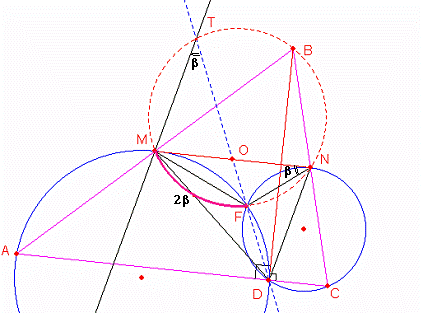
Ahora observamos que la circunferencia circunscrita al triángulo DNC desde el punto O (OFD es una secante y ON es una tangente) luego se cumple que esto implica que los ángulos del triángulo OND los ángulos finalmente demostramos que las rectas que pasan por los puntos M, T y D, N son paralelas

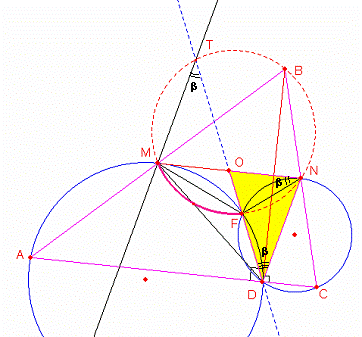
Ahora demostraremos que las rectas que pasan por los puntos M, D y T, N son también paralelas

Según el gráfico observamos que: ,

Y como el ángulo OMF es semi Inscrito entonces el arco con esto determinamos que las rectas que pasan por los puntos T, N y M, D son paralelas

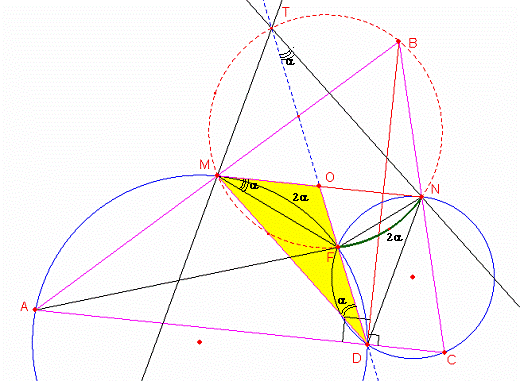
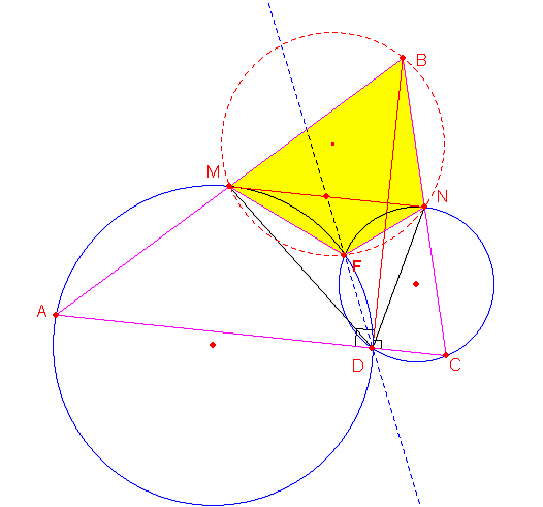
Finalmente el cuadrilátero MTND es un paralelogramo donde TD y MN son sus diagonales por lo tanto el punto O es el punto medio

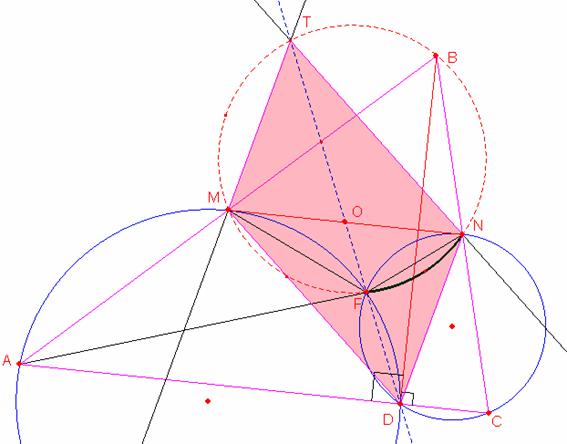
Figure PRO310.fig

Applet created on 1/05/06 by william with CabriJava

Prof.: William Rodríguez chamache