Problema 313 de triánguloscabri

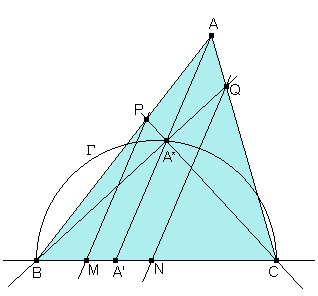
Sea ABC un triángulo no rectángulo. Trazamos, la ceviana arbitraria AA' desde A al lado BC.

Construimos el triángulo A*BC rectángulo en A* , punto que está en la ceviana AA', del que prolongamos su catetos hasta que corten en los puntos P y Q, a los lados AB y AC, respectivamente.

Los puntos M y N sobre el lado BC se obtienen como intersección de las paralelas por P y Q, a la ceviana AA',
respectivamente.

Construimos los siguientes puntos :

  • X(A), es la intersección de PN y QM;    D es la intersección de PQ y BC;
  • U es la intersección de PM y BQ;    V es la intersección de QN y PC;
  • E es la intersección de UC y QN;     F es la intersección de PN y QB;
  • G es la intersección de PC y QM;     H es la intersección de BV y PM;
  • I es la intersección de UN y BV;     J es la intersección de UC y BV;
  • K es la intersección de UC y PN;     Y(A), es la intersección de UN y MV;
  • T es la intersección de UC y MQ;     S es la intersección de BV y PN;
  • Z(A), la intersección de HQ y PE.

Demostrar que:

a) las rectas AA', PN, QM son concurrentes en X(A); 
b) las rectas AA', UN, MV son concurrentes en Y(A);
c) las rectas AA', HQ, PE, son concurrentes en Z(A);
d1) los puntos D, F y G están alineados;
d2) los puntos D, T y S  están alineados;
e) los puntos M,  T, X(A), G y Q están alineados;
f1) los puntos P, F, X(A), S, K y N están alineados;
f2) los puntos B, H, I, J, S y V están alineados;
f3) los puntos C, E, K, T, J y U  están alineados;
g1) los puntos H,  Z(A) y Q están alineados;
g2) los puntos P, Z(A) y E están alineados.
Propuesto por Juan Bosco Romero Márquez

Solución de Francisco Javier García Capitán

Consideraciones iniciales

Si tomamos A' sobre BC y luego construimos A* sobre AA' de manera que BA*C sea rectángulo, A* deberá estar en la intersección de AA' con la circunferencia G de diámetro BC.

Para hacer más fácil el cálculo de la intersección con la circunferencia, en lugar de considerar a A* como punto de partida, consideraremos un punto Q variable en CA, y a partir de él obtendremos A* como la segunda intersección de G con la recta BQ. Una vez hallado A* podemos hallar A' y todos los demás puntos.

 

 

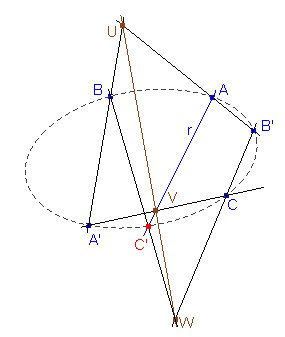La segunda intersección

La geometría proyectiva proporciona una forma sencilla (usando sólo rectas) de obtener la intersección de una cónica dada por cinco puntos y una recta que pasa por uno de ellos.

Si la cónica pasa por los puntos A, B, C, A', B' y queremos hallar el otro punto C' en que corta a la cónica una recta que pasa por A, podemos considerar lala homografía que lleva A, B, C en A', B', C'. Entonces los tres puntos

U = AB' Ç A'B, V=CA'Ç C'A =CA'Çr, W = B'C Ç BC'

deberán estar alineados en el eje de homografía, y podemos hallar el punto uscado como C' = r ÇBW.

Para una explicación más a fondo, ver el documento de Jose María Pedret:

SI SOLO TENEMOS LOS CINCO PUNTOS QUE DEFINEN UNA CONICA (Un enfoque práctico para las construcciones con regla y compás)


Introducción de los primeros datos

Para hacer cálculos con Mathematica con lo que hemos dicho hasta aquí invocamos al cuaderno Baricentricas.nb y definimos una función para hallar el punto de intersección de dos rectas AB y CD:

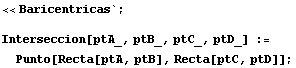
También definimos una función para obtener la segunda intersección de una recta con una cónica (nosotros la usaremos con una circunferencia):

Ahora usaremos esta función para obtener el punto A* a partir de un punto cualquiera Q sobre CA. Para usar la función SegundaInterseccion necesitamos cinco puntos de la circunferencia. Tenemos dos puntos B y C. También están en la circunferencia los pies Bh y Ch de las alturas desde B y C, respectivamente. Por último consideramos el punto antípoda B2 de Bh. Esto nos permite calcular A* (representado aquí como ptAe):

Ahora podemos calcular los demás puntos del enunciado. Estos ...

... y todos los demás:

Una vez hecho esto, podemos usar una sola instrucción para comprobar que son ciertas todas las afirmaciones del enunciado: