Problema 314 de triánguloscabri

Sea ABC un triángulo cualquiera. Con un punto D se obtiene un cuadrilátero ABCD. Construir las bisectrices de los ángulos DAB y DCB. ¿Dónde colocar el punto D para que las bisectrices de DAB y DCB sean paralelas? Estudiar esta situación y justificar vuestras conjeturas.

Esta actividad comienza por una exploración que puede ser beneficiosa con la ayuda de un logicial como Cabri-Géomètre.

Clapponi, P. (1994): Activité .. des bissectrices paralleles. Petit X 35

Solución de Francisco Javier García Capitán

Exploración con Cabri-Géomètre

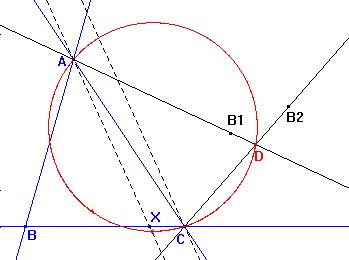
Situemos un punto cualquiera X sobre BC y pensemos en AX como la bisectriz del ángulo DAB. Entonces la recta AD será la recta simétrica de AB respecto de AX.

Ahora trazamos la paralela por C a AX, que deberá ser la bisectriz del ángulo DCB, por lo que la recta CD es la simétrica de CB respecto de esta paralela.

Entonces obtenemos el punto D como intersección de las rectas AD y CD.

Usando la herramienta Lugar geométrico de Cabri vemos que el lugar de D es una circunferencia que pasa por A y C.

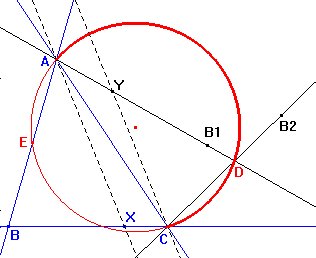
Estudio de la situación y justificación de los resultados obtenidos

Observemos la figura:

Por ser ÐBAX = ÐXAD = ÐCYD y ÐAXB =ÐYCB=ÐYCD los triángulos ABX e YDC son semejantes, resultando que ÐADB (= ÐABC) es constante, y D debe estar en el arco capaz de AC para para el ángulo B.

En la figura hemos utilizado que D y B están en distintos lados de la recta CA. Si D y B estuvieran en el mismo lado, las bisectrices en lugar de ser paralelas serían perpendiculares.
En la figura uno de esos puntos es E, construido de manera que CBE es isósceles. En ese caso la bisectriz de ECB es perpendicular a la recta BA, que es precisamente la bisectriz del ángulo (nulo) EAB.
La observación anterior puede servir para obtener directamente la circunferencia ABD sin necesidad de la herramienta Lugar geométrico.