De investigación. Propuesto por José Carlos Chavez Sandoval, estudiante peruano de Matemática Pura en la Universidad Nacional Mayor de San Marcos

Problema 315

Dado un triangulo ABC, y una cónica, sea A'B'C' el triangulo polar de ABC con respecto a la conica. Demostrar que ABC y A'B'C' estan en perspectiva.

Yiu, P. (2001). Introduction to the Geometry of the Triangle,version 2.0402, Summer 2001.

http://www.math.fau.edu/yiu/Geometry.html

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de agosto de 2006)

SEGUNDA SOLUCIÓN

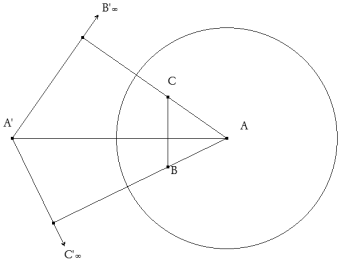
figura 1

Mediante una homología la cónica se transforma en un círculo (ver figura) y uno de los lados de uno de los triángulos en la recta impropia. Si A'B'_∞C'_∞ es ese triángulo, B'_∞C'_∞ es la recta impropia, el otro triángulo es ABC, siendo A el centro del círculo (polo de la recta impropia), BC es la polar de A', luego AA' es perpendicular a BC. Por otra parte, C y B son los polos de A'B'_∞ y A'C'_∞, luego AC y AB son perpendiculares a A'B'_∞ y A'C'_∞. Se sigue que AA', BB'_∞ y CC'_∞ son las alturas del triángulo ABC, que se cortan en su ortocentro. Por tanto, ABC y A'B'_∞C'_∞ son homológicos, luego también lo son los triángulos del enunciado.

NOTA

Esta solución puede encontrarse en el problema nº 60 de GEOMETRÍA ANALÍTICA Y PROYECTIVA DEL PLANO (2ª edición) de DARIO MARAVALL CASESNOVES. Editorial Dossat. Madrid 1965.