Problema 315 de investigación.

Propuesto por José Carlos Chavez Sandoval, estudiante peruano de Matemática Pura en la Universidad Nacional Mayor de San Marcos

Dado un triangulo ABC, y una cónica, sea A'B'C' el triangulo polar de ABC con respecto a la conica. Demostrar que ABC y A'B'C' estan en perspectiva.

Yiu, P. (2001). Introduction to the Geometry of the Triangle,version 2.0402, Summer 2001.

http://www.math.fau.edu/yiu/Geometry.html

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de junio de 2006)

SOLUCIÓN

figura 1

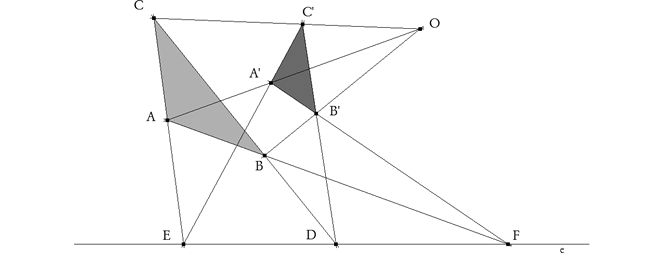
Llamamos E al punto de intersección de CA con C'A'.

Llamamos F al punto de intersección de AB con A'B'.

Si llamamos D al punto de intersección de BC con B'C', hay que demostrar que D está sobre EF.

Los puntos B y E son conjugados respecto a la cónica, ya que E se encuentra en A'C' que es la polar de B; del mismo modo podemos asegurar que C y F también son conjugados.

Así en el cuadrilátero que forman BC, CA, AB y EF, dos pares de vértices opuestos B y E, C y F son conjugados; entonces el tercer par también es conjugado, A y D donde BC encuentra a EF.⁽¹⁾

B'C' la polar de A entonces debe pasar por D ⁽²⁾; así BC y B'C' se encuentran en un punto D sobre EF(c.q.d.).

Nota

Esta propiedad de los triángulos conjugados respecto a una cónica, aparece abundantemente en la literatura, especialmente donde se estudie la transformación por polares recíprocas. (Lo que hace que la solución que presento no sea original.

⁽¹⁾ Se usa el siguiente teorema debido a HESSE

Si los extremos de cada una de las dos diagonales de un cuadrilátero completo son conjugados respecto a una cónica dada, los extremos de la tercera diagonal también son conjugados respecto a la misma cónica.

⁽²⁾ Dos puntos son conjugados respecto a una cónica si la polar del uno pasa por el otro.