De investigación

Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Problema 317

Siguen , ha hb hc, les tres altures del triangle ABC tals que ha=hb+hc.

La recta que passa pels peus de les bisectrius interiors dels angles B i C passa pel baricentre del triangle.

Oposicions d’Eivissa 2002.

Sean ha hb hc, las tres alturas del triángulo ABC tales que ha =hb+hc.

La recta que pasa por los pies de las bisectrices interiores de los ángulos B y C pasa por el baricentro del triángulo.

Oposiciones Ibiza 2002.

Solución de María Calvo Cervera, estudiante de primero de Matemáticas en Granada:

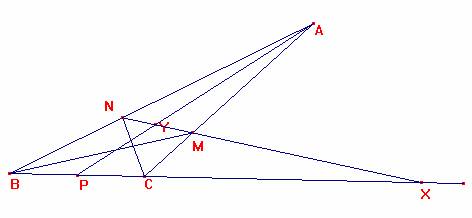
Se tiene que:

2S = a ha = b hb = c hc, se tiene , y por tanto la condición del enunciado queda

Consideremos ahora el triángulo ABC, donde M y N son los pies de las bisectrices correspondientes a los ángulos B y C respectivamente. Por el teorema de la bisectriz:

La recta que pasa por M y N corta a la recta BC en X y por el teorema de Menealo se tiene:

Esto último nos dice que X es el pie de la bisectriz externa del vértice A y por tanto se cumple:

Consideremos ahora el triángulo APB, siendo el P el punto medio de BC, y apliquemos el teorema de Menealo con los puntos X, M y Y, siendo el Y el punto de corte de la recta AB con MN. Se tiene:

Simplificando se llega a:

Como ab + ac = bc:

AY=2YP

Se tiene que la recta AP es la mediana y por tanto el punto Y es el baricentro.c.q.d.