De investigación

Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Problema 317

Siguen , ha hb hc, les tres altures del triangle ABC tals que ha=hb+hc.

La recta que passa pels peus de les bisectrius interiors dels angles B i C passa pel baricentre del triangle.

Oposicions d’Eivissa 2002.

Sean ha hb hc, las tres alturas del triángulo ABC tales que ha =hb+hc.

La recta que pasa por los pies de las bisectrices interiores de los ángulos B y C pasa por el baricentro del triángulo.

Oposiciones Ibiza 2002.

Solución del director

Primera parte.

h_a a = h_b b = h_c c = 2 [ABC] de donde h_c/ h_b =b/c

h_a = h_b + h_c

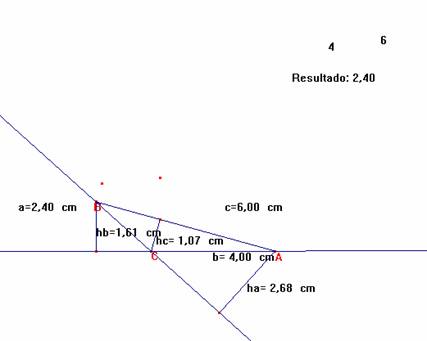
h_b a + h_c a = h_b b -> a + (h_c / h_b )a=b.

a+ (b/c)a=b -> 1/b + 1/c = 1/a.

Segunda parte: para que G, Wc y Wb estén alineados,

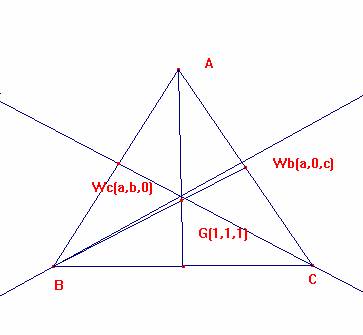
ha de ser, el determinante formado por las coordenadas baricéntricas nulo:

| (1,1,1), (a,b,0), (a,0,c)| = 0,

Es decir, bc – ba – ac=0, es decir, 1/a = 1/c+ 1/b.

Luego ambas condiciones son equivalentes.

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla