Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Problema 317

Sean ha hb hc, las tres alturas del triángulo ABC tales que ha =hb+hc.

La recta que pasa por los pies de las bisectrices interiores de los ángulos B y C pasa por el baricentro del triángulo.

Oposiciones Ibiza 2002.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de julio de 2006)

SOLUCIÓN

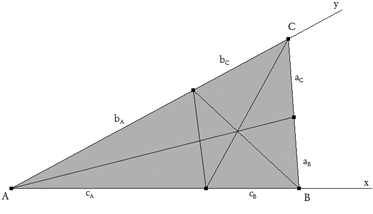
Dibujamos un triángulo ABC, sus bisectrices y los segmentos que éstas determinan en los lados.

figura 1

TEOREMA DE LAS BISECTRICES

LADOS DEL TRIÁNGULO

ÁREA DEL TRIÁNGULO

CONDICIÓN DEL ENUNCIADO

EXPRESIÓN DE LOS SEGMENTOS QUE DETERMINAN LAS BISECTRICES EN FUNCIÓN DE LOS LADOS

Con los datos anteriores obtenemos

RECTA POR LOS PIES DE LAS BISECTRICES

En unos ejes oblicuos la recta pasa por el punto (c_A,0) y el punto (0,b_A) lo que nos da la ecuación de la recta como

BARICENTRO

SUSTITUIMOS LAS COORDENADAS DEL BARICENTRO EN LA RECTA

CONCLUSIÓN

G está sobre la recta (c.q.d.)