De investigación

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 318

18. Si en el triángulo ABC el ángulo A=60º , y llamamos O al punto de concurso de las rectas que unen los vértices A,B,C a los centros A´, B´, C´, de los triángulos equiláteros construidos exteriormente  a los lados BC, CA, AB; demostrar que

BO/ BB´ + CO/CC´= 1,  BO/BB´: CO/CC´= AB/ AC,   (BO/BB´)(CO/CC´) = (1/2) ( AO/AA´)

Alba, L. de (1902)  "Revista Trimestral de matemáticas", Año, II, N.5, 

Solución del director.

Apartado 1

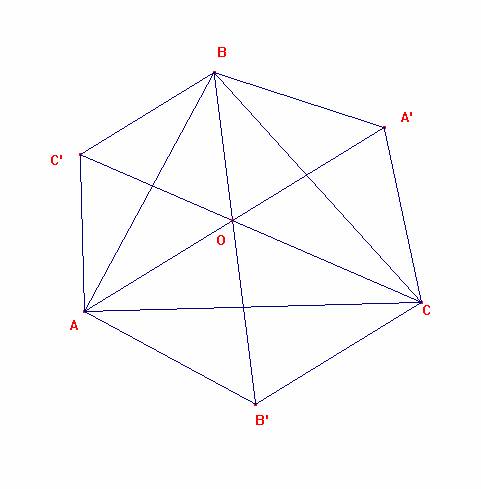
BO/ BB´ + CO/CC´= 1

Debemos demostrar que BO/ BB´ = 1 - CO/CC´= C’O/CC’

Los segmentos BC’ y CB’ son paralelos pues

1.- <ACB’ =30º

2.- <CAC’=60º+30º=90º

3.- <AC’B=120º

4.- por 2.- y 3.- el ángulo que formarían la recta AC con C’B es de 30º.

Por ser paralelos B C’ y C B’, los triángulos BC’O y CB’O son semejantes.

Por ello, es BO/C’O=OB’/OC=BB’/CC’, luego BO/ BB´ = C’O/CC’ cqd

Apartado 2

Hemos de demostrar que BO/BB´: CO/CC´= AB/ AC.

Por el apartado 1, es:

BO/BB´: CO/CC´= C’O/CC’: CO/CC´ = C’O/CO.

Por ser, como vimos antes, C’BO semejante a CB’O, es C’O/CO = C’B/B’C.

Los triángulos AC’B y AB’C son isósceles 30º 120º 30º, y por ello semejantes, luego es

C’B/B’C = AB/AC.

Por todo ello, es

BO/BB´: CO/CC´= C’O/CC’: CO/CC´ = C’O/CO = C’B/B’C = AB/AC, cqd

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla