De investigación

Propuesta de José Carlos Chávez Sandoval, estudiante peruano de Matemática Pura en la Universidad Nacional Mayor de San Marcos

Problema 319

Dado el triángulo ABC, tal que m<ABC=90º. Sea Y en AC tal que los triángulos ABY y YBC tienen el mismo inradio, demostrar que BY^2=[ABC], donde [ABC] es el área del triángulo ABC. Además generalizarlo en función de BY y el ángulo ABC cuando este es diferente de 90º.

Sug. Usar cotangente del ángulo mitad.

Chávez, J.C. (2006): Comunicación personal.

Solución y notas de Juan Carlos Salazar

Véase la figura

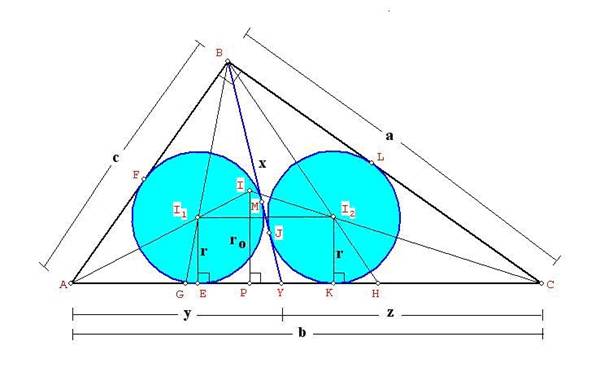
Procederemos a tratar de establecer una relación para BY en función de los catetos.

Sean (I₁, r₁), (I₂, r₂) los incírculos de los triángulos ABY y BYC, determinados por la ceviana BY en el triángulo rectángulo ABC, donde BG y BH son bisectrices de <ABY y <YBC respectivamente. AI₁ y CI₂ se cortan en I, incentro de ABC. Para este caso r₁=r₂=r, AB=c, BC=a, AC=b, r₀ = inradio de ABC, AY=y, YC=z, AY=x, y sea h la altura sobre AC.

Al aplicar el teorema del incentro en los triángulos ABY y BYC:

BI₁/I₂G=(x+c)/y=BI₂/I₂H=(x+a)/z , ya que I₁I₂//AC. Luego:

y = b(x+a)/(a+c+2x); z = b(x+c)/(a+c+2x)

Si aplicamos el teorema de Stewart al triángulo ABC con ceviana BY:

b.x² = y.a² + z.c²-yzb

Al reemplazar y y z en esta última relación obtendremos un ecuación para x en función de los lados a, b y c, sabiendo que b= (a²+c²)^1/2, pero que desafortunadamente no es posible resolverla por métodos tradicionales.

Pero tenemos otra alternativa, establecemos una relación de áreas:

[ABC] = [ABY] + [BYC]

[ABC] = (c+x+y)r/2 + (x+a+z).r/2=(a+b+c+2x)r/2

x = ac/ (2r) – (a+b+c)/2... (1)

Luego usaremos una relación para los inradios de los triángulos parciales determinados por una ceviana, la altura h y el inradio r₀ de ABC:

2/h=1/r₁+1/r₂-r₀/ (r₁r₂)

En este caso: r₁ = r₂ = r:

2/h=2/r-r₀/r²

r²-hr+hr₀=0

Resolviendo esta ecuación: r = (h/2)-(h/2).(1 - 4r₀/h) ^1/2

También: r₀/h=b/ (a+b+c). Luego:

r=(h/2)-(h/2).[1 - 4b/(a+b+c)] ^1/2

r =(h/2)-(h/2).[(a+c-3b)/ (a+b+c)] ^1/2

Reemplazando: h = ac/b

r = ac / (2b)- [(ac) / (2b)]. [(a+c-3b)/(a+b+c+)]^1/2

Esta última expresión la reemplazamos en (1) para obtener x, que como podemos inferir no será una expresión sencilla.

Sin embargo, al utilizar el siguiente resultado más general (*):

Si en un triángulo ABC, se traza la ceviana BY, de tal modo que los incírculos de ABY y BYC son iguales, luego BY=(s(s-b))^1/2.

Para este caso: r₀=(s-b), luego sr₀ = s(s-b) = ac/2, por lo tanto:

BY = x = (ac/2)^1/2

[ABC]= BY²

(*) Agradezco a Darij Grinberg por facilitarme esta información. Ver:

http://www.mathlinks.ro/Forum/viewtopic.php?t=32586