De investigación

Propuesto por José María Pedret. Ingeniero naval. (Esplugas de Llobregat, Barcelona)

Un problema muy atractivo es el recíproco del 315 y que desde aquí lo propongo a RICARDO BARROSO por si tiene a bien el publicarlo  

Problema 320 .- "Dados dos triángulos perspectivos ABC y A'B'C', construir (si existe) la cónica respecto a la que son perspectivos." Pedret, J.M. (2006) Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Según vimos en el problema 315, si dos triángulos son polares respecto de una cónica, son perspectivos, resolveremos el problema actual, encontrando una cónica para la cual los pares de puntos (B,C’); (B’,C); (A,B’); (A’,B); (A,C’) y (A’,C) son conjugados respecto de ella. Analicemos lo que significan estas condiciones.

Si tenemos la cónica como una matriz M simétrica de orden 3, la condición de conjugación del primer par se expresa por M(B,C’)=0, una ecuación lineal homogénea de los coeficientes de la matriz. Es equivalente a dar un punto de la cónica; en este caso la ecuación es de la forma M(P,P)=0.

También podemos verlo desde otro enfoque, la cónica queda perfectamente determinada dando cuatro puntos y el par conjugado utilizando el teorema del cuadrivértice de Desargues. La recta definida por el par de conjugados corta a los pares de lados opuestos del cuadrivértice formado por los cuatro puntos en pares recíprocos de una involución. Los puntos dobles de la misma son puntos de la cónica, y así podríamos tener los suficientes para poder determinarla por completo. (Si la cónica no tiene puntos en la recta, o sea la involución es elíptica, hay recursos para hallar la polar de un punto de la involución y proseguir hasta determinar la construcción de la cónica, pero esto es desviarse demasiado del problema. Quién desee más detalles puede consultar la excelente obra Geometría Métrica, P. Puig Adam, que dedica su segundo volumen a la Geometría Proyectiva).

Así pues podemos considerar que tenemos condiciones suficientes para asegurar la existencia de una cónica en la que sean conjugados los cinco primeros pares de puntos que hemos formado a partir de los vértices de los dos triángulos.

Sólo resta ver que el sexto par, (A’,C), también es conjugado respecto de esta cónica.

Usaremos la propiedad (P1) del problema 315: si dos pares de vértices opuestos de un cuadrilátero completo son conjugados con respecto a cierta cónica, también lo es el otro par.

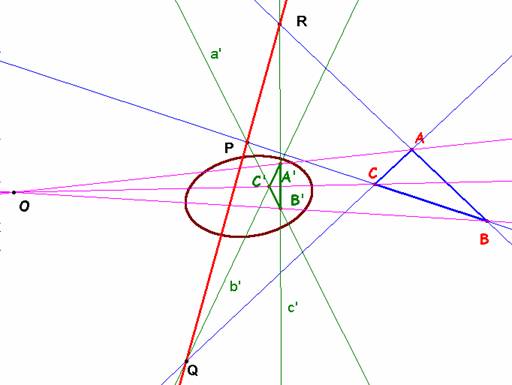
Tomando el cuadrilátero completo formado por las rectas BB’, CC’, BC y B’C’, en el que son opuestos los pares(B,C’); (B’,C) y (O,P). El par (O,P) lo forman puntos conjugados.

Si ahora se toman BB’, AA’, BA y B’A’ resultan conjugados O y R (además de (A,B’) y (A’,B)). De estas dos deducimos que la polar del punto O (vértice de la homología) es la recta PQR (eje de la misma).

Considerando, por último, el cuadrilátero definido por AA’, CC’, AC y A’C’ en el que son opuestos (O,Q); (A,C’) y (A’,C), la conjugación de los dos primeros implica la del último, y con ello la sexta relación de conjugación que faltaba queda demostrada y concluimos.