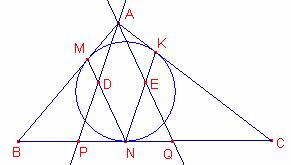
Problema 322
La circumferència inscrita al triangle 
és tangent als costats
en els punts M, N, K
respectivament.
La recta paral·lela a NK que passa per A talla MN en
el punt D. La recta paral·lela a MN que passa per A talla NK en E.
Proveu que la recta DE bisecta els costats 
del triangle .
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de
Xest (València) (en valenciano) :
Per ser M, K punts de tangència 
Per ser M, N punts de tangència 
Per ser K, N punts de tangència 
.
Aleshores els triangles 
, 
,
són isòsceles.
Siga r la recta paral·lela a NK que passa per A.
Aquesta recta talla el costat 
en el punt P.
, 
són paral·lels,
aleshores els triangles , 
són semblants.
Aplicant el teorema de Tales:
és a dir, 
, 
són paral·lels,
aleshores els triangles , 
són semblants.
Aplicant el teorema de Tales:
és a dir, 
, 
són paral·lels,
aleshores els triangles 
, 
són semblants.
La raó de semblança és:
.
Aleshores E pertany a la paral·lela mitjana del
triangle és a dir a la
paral·lela mitjana del triangle .
Anàlogament D pertany a la paral·lela mitjana de
triangle .