Problema
322.
La circunferencia
inscrita en el triángulo 
es tangente a los lados
en los puntos M, N, K
respectivamente.
La recta
paralela a NK que pasa por A corta MN en el punto D. La recta paralela a MN que
pasa por A corta NK en E.
Probar que
la recta DE bisecta los lados 
del triángulo .
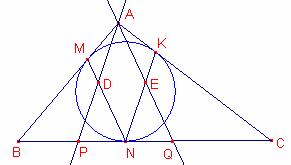
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (Valencia)
Por ser M,
K puntos de tangencia 
Por ser M,
N puntos de tangencia 
Por ser K,
N puntos de tangencia 
.
Entonces los
triángulo 
, 
,
son isósceles.
Sea r la
recta paralela a NK que pasa por A.
Esta recta
corta el lado 
en el punto P.
, 
son paralelos, entonces
los triángulo , 
son semejantes. Aplicando
el teorema de Tales:
es decir, 
, 
son paralelos, entonces
los triángulos , 
son semejantes. Aplicando
el teorema de Tales:
es decir, 
, 
son paralelos, entonces
los triángulo 
, 
son semejantes.
La razón
de semejanza es:
.
Entonces E
pertenece a la paralela media del triángulo , es decir a la paralela media del triángulo .
Análogamente
D pertenece a la paralela media de triángulo .