Problema
323.
Dado el
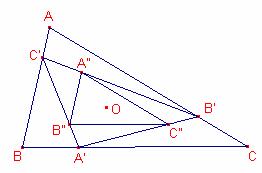
triángulo 
se inscribe en el otro triángulo 
y en el triángulo anterior se inscribe otro
triángulo 
que tiene los lados paralelos al triángulo
inicial . Determinar el área del triángulo en función de las áreas de los triángulos , 
.
Solución de Ricard
Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (Valencia)
Sean 
las áreas de los triángulos
, respectivamente.
Los triángulos
n, son homotéticos ya que los lados son paralelos.
Sea O el
centro de homotecia.
La razón
de semejanza de los triángulos es la raíz cuadrada de la proporción de las áreas:
Sea 
la altura del triángulo
. Sea 
la altura del triángulo
Los triángulos
, están en posición de
Tales y la razón de semejanza es . Por tanto, 
.
La altura
del triángulo 
es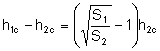 
Sean 
las alturas de los triángulos 
, 
.
Análogamente
la altura del triángulo 
es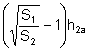 
, la altura del triángulo 
es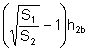 
.
Calculemos
el área del triángulo :
.
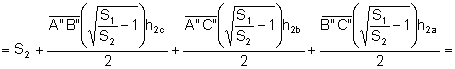
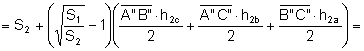
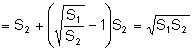Entonces
el área del triángulo es media geométrica de
las áreas de los triángulos , .