Para el aula

Problema 326

34. ABC es un triángulo rectángulo en B. Sobre BC hacia el exterior del triángulo se construye un triángulo equilátero BCD, y se construye el segmento AD. Demostrar que [BCD]=[ACD]-[ABD], donde [BCD], [ACD] y [ABD] son las áreas de los triángulos correspondientes.

Aref, M.N., Wernick,W. (1968): Problems &Solutions in Euclidean Geometry. Dover Publications, Inc, New York. (pag. 58)

Solución del director

Sea la situación geométrica propuesta.

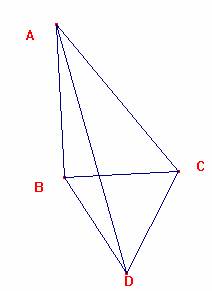
Tracemos DE perpendicular a BC, y AE. Obtenemos así seis triángulos:

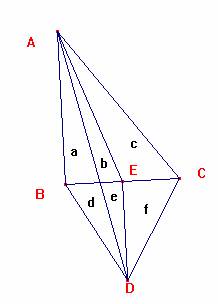
Sean a, b, c, d, e, y f las áreas de cada uno de ellos.

Hemos de ver que: d+e+f = b+c+e+f – a – d

2 d + a = b+c

Al ser ED paralela a AB las áreas de ABE y ABD coinciden.

Ello nos lleva a que d=b

Luego hemos de ver que d+a=b+a=c, lo que es cierto al ser E punto medio de BC, cqd

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla