Problema 327

Dado un triangulo ABC, sea un punto P en su plano y sean x=AP, y=BP, z=CP. Demostrar que:

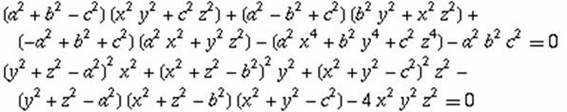
http://mathworld.wolfram.com/TripolarCoordinates.html (Euler 1786).

Solución de José Carlos Chávez Sandoval, estudiante peruano de Matemática Pura en la Universidad Nacional Mayor de San Marcos

Dado un triangulo ABC, un punto P en su interior.

Sean AP=x, BP=y, CP=z.

Sean k=medida de <APC y l=medida de <CPB.

Por el teorema de cosenos tenemos:

c^2=x^2+y^2-2xycosk                              I.

a^2=y^2+z^2-2yzcosl                               II.

b^2=x^2+z^2-2xzcos(k+l)                         III.

Por la formula del ángulo compuesto tenemos que cos(k+l)=cosk cosl-senk senl

Reemplazando en III. senksenl=coskcosl+(b^2-x^2-z^2)/2xz

y elevando al cuadrado se sigue que

cos^2kcos^2l + (b^2-x^2-z^2)^2/4x^2z^2 + coskcosl(b^2-x^2-z^2)/2xz= sen^2(k).sen^2(l)=(1-cos^2(k))(1-cos^2(l))

y reemplazando I. y II. se siguen los resultados.