De investigación
Problema 329
Propuesto
por Juan Bosco Romero Márquez profesor colaborador de
la Universidad de Valladolid
Demostrar que un triángulo cuyos ángulos B y
C satisfacen la igualdad
Es rectángulo.
[Ampliación del proponente: ver qué tipo de
triángulo es si se tienen las posibles desigualdades]
IMO Shortlist 1967.
Poland. 5
Solución de Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid) (11 de agosto de 2006)
Multiplicando a ambos lados de la ecuación por el denominador del primer miembro y agrupando senos y cosenos es fácil obtener:
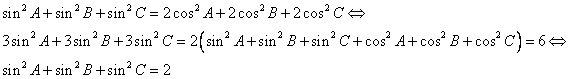
Y utilizando el teorema del seno vemos que:
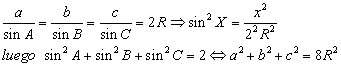
Podemos suponer sin pérdida de la
generalidad que 
y utilizando ahora el teorema del coseno
obtenemos:
Puesto que 
, tenemos que el signo de esta expresión depende de la
relación 
.
En caso de que 
.
En caso de que 
. Por último, si 
y además tenemos que
por ser 
los ángulos de un
triángulo 
, y por ello 