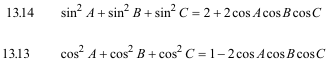De investigación. Propuesto por Juan Bosco Romero Márquezprofesor colaborador de la Universidad de Valladolid

Problema 329

Demostrar que un triángulo cuyos ángulos B y C satisfacen la igualdad

Es rectángulo. [Ampliación del proponente: ver qué tipo de triángulo es si se tienen las posibles desigualdades] IMO Shortlist 1967. Poland. 5

http://www.mathlinks.ro/Forum/resources.php?c=1&cid=17&year=1967&sid=183024c22942408a0b5a9f0b3955605d

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (5 de julio de 2006)

SOLUCIÓN

Si tomamos la igualdad del enunciado

en TRAJAN LALESCO (La géométrie du triangle. Vuibert. 1952. Paris) obtenemos del capítulo 13

y si sustituimos el 2 del enunciado por 2+ε

Si ε=0 

Uno de los cosenos se anula. .El triángulo es rectángulo

Si ε>0

Todos los cosenos son positivos y por tanto todos los ángulos son agudos. El triángulo es acutángulo.

Si ε<0

Uno de los cosenos es negativo y por tanto todos uno de los ángulos es obtuso. El triángulo es obtusángulo.