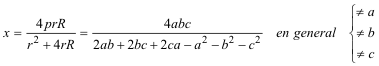De investigación Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 330

Sean T y T´ dos triángulos que tienen el mismo perímetro y que verifican que, R/R´= r/r´, donde R, R´y r, r´ son los radios de los círculos circunscritos e inscritos, respectivamente a T y T. Demostrar que T y T´ son congruentes.

Romero, J.B. (2006) Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (25 de julio de 2006)

DISCUSIÓN

Si dos triángulos son congruentes sus lados son iguales.

Sean a, b, c los lados del primer triángulo. El polinomio cuyas raíces son los lados del triángulo es

Con el semiperímetro

Con el área del triángulo

Con el radio del círculo inscrito

Sustituyendo en el polinomio

Para el segundo triángulo su polinomio es

Pero el enunciado nos dice

de donde

y comparando con Q(x)

Estos polinomios sólo tienen las mismas raíces (los triángulos son congruentes) si

el valor -1 no puede ser ya que λ es una razón de lados. Además también se igualarían si

fuera raíz de Q(x) lo que en general no es cierto.

CONCLUSIÓN

En el enunciado falta indicar que

para ser correcto.