Sofismas geométricos.- Hoy en día todo el mundo tiene algunas nociones de geometría e incluso una idea general de los Elementos de Euclides, pero se conoce menos que las obras de este gran geómetra estaban completadas en su origen por ejercicios divididos en tres series. Las dos primeras comprendían los teoremas y problemas fáciles y la tercera era una colección de artificios geométricos de los que se trataba de encontrar los errores.    

La colección de artificios preparada por Euclides se ha perdido, y no poseemos ninguna información de los razonamientos erróneos empleados, pero para poder dar una idea de este género de cuestiones presentamos a continuación dos o tres demostraciones conducentes a consecuencias manifiestamente absurdas y que posiblemente divertirán a aquellos para los que sean nuevas. Dejamos al ingenio de nuestros lectores el cuidado de descubrir los errores del razonamiento.

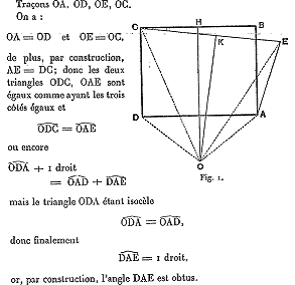
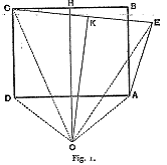
Primer sofisma. Demostrar que un ángulo recto es igual a un ángulo obtuso.- Sea un rectángulo ABCD; por el vértice A llevemos una recta AE exterior al rectángulo, igual a AB o DC y formando como muestra la figura, un ángulo agudo EAB con el lado AB. Tracemos CE y tomemos los puntos medios K  y H de las rectas CE y CB. Las perpendiculares elevadas a estas rectas en los puntos K y H se encontrarán necesariamente en un cierto punto O debido a que CB y CE no son paralelas. 

Tracemos OA, OD, OE, y OC.

Se tiene :

OA=OD y OE=OC.

Además, por construcción, AE=DC, pues los dos triángulos ODC y OAE son iguales teniendo los tres lados iguales y siendo <ODC=<OAE, o aún, <ODA+ 1 recto= <OAD+<DAE, de donde finalmente, <DAE=1 recto, pues por construcción, el ángulo DAE es obtuso.