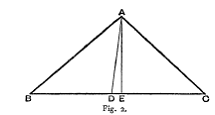
Segundo sofisma. Demostrar que un segmento de un lado de un triángulo es igual al lado completo. Sea ABC un triángulo cualquiera; para fijar ideas supongamos que el ángulo B es agudo y el ángulo A es mayor que el ángulo C

Por el vértice A llevemos en el interior del triángulo la recta AD haciendo con el lado AB un ángulo BAD igual al ángulo C y abatamos la perpendicular AE sobre BC.

Los triángulos ABC y ABD son equiángulos y por tanto semejantes, por lo que se tiene que

[ABC]/[ABD]=AC²/AD²

Además, al tener la misma altura, la relación de áreas es igual a las de las bases, de donde se tiene la relación [ABC]/[ABD]=BC/BD

La comparación entre las dos relaciones nos da:

(1)   AC²/AD² =BC/BD, o

AC²/BC=AD² /BD, o sea:

     AC²=AB² + BC² -2BC BE

Y

AD²=AB² + BD² -2BD BE,

Y se llega, reemplazando en (1), a

(AB² + BC² -2BC BE)/BC= (AB² + BD² -2BD BE)/BD, de donde:

AB²/BC  + BC – 2 BE =AB²/BD + BD – 2BE

o después de una simplificación y transposición,

AB²/BC  -BD =AB²/BD – 2BC,

Y al fin,

(AB² –BD BC )/BC= (AB² – BD BC)/BD, de donde se deduce este resultado inadmisible, BC=BD