Problema 331 de triánguloscabri

Solución de Francisco Javier García Capitán

Presentamos dos soluciones una algebraica/geométrica y otra geométrica

Primer método (usando el álgebra)

Soluciones de una ecuación de segundo grado

Vamos a resolver el problema atacándolo desde un punto de vista algebraico. Para ello necesitaremos saber resolver gráficamente un sistema del tipo

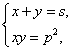(1)

o lo que es lo mismo hallar gráficamente las soluciones de la ecuación

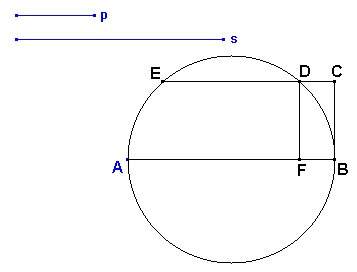
Para ello construimos una circunferencia con diámetro AB = s, y por uno de sus extremos (B en la figura) levantamos una perpendicular BC = p. La paralela por C a AB cortará, en general, en dos puntos D y E a la circunferencia. Por uno de ellos, por ejemplo D, trazamos una perpendicular a AB, que corta a ésta en F. Entonces los segmentos x = AF e y = FB cumplen (1).

Si el producto xy debiera ser igual al producto de dos cantidades m y n, bastaría hallar previamente la media geométrica p de m y n.

Solución algebraica

Si son conocidas la hipotenusa a y la suma s de los catetos b y c, tendremos

Entonces b y c pueden obtenerse como las soluciones de (1) siendo s la suma dada y p la media geomeétrica de las longitudes (s+a)/2 y (s-a).

Construcción con Cabri

Las consideraciones anteriores llevan a la siguiente construcción:

1. Trazamos una recta y sobre ella situamos el vértice C.
2. Marcamos los puntos D tal que CD = a + s y el punto medio E de CD.
3. Marcamos por el otro lado el punto F tal que FC= s-a.
4. Trazamos la circunferencia de diámetro FE y levantamos por C una perpendicular a FE que corta a la circunferencia en I.
5. Trazamos otra circunferencia de diámetro HC =s=b+c y una paralela a HC por I que corta a dicha circunferencia en J y K.
6. La proyección ortogonal de J sobre FE da el punto B y una perpendicular BA = BH a AC da el punto A.

Segundo método (análisis geométrico)

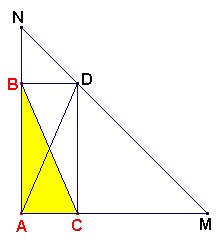Vamos a suponer construido el triángulo pedido ABC y vamos a tratar de situar en ella los datos que nos da el problema.

Completamos cada uno de los catetos con el otro, teniendo un triángulo rectángulo AMN isósceles cuyos lados iguales miden s.

Las paralelas por B y C a AC y AB respectivamente se cortan en un punto D sobre MN y es evidente que AD = BC = a, lo que permite obtener el punto D con los datos del problema:

1. Dibujamos el triángulo isósceles AMN rectángulo en A.
2. Con centro en A y radio a trazamos un arco que determina D sobre MN (habría en general dos puntos, pero dando lugar a dos triángulos solución iguales).
3. Trazamos una perpendicular a AM por C que da lugar y tenemos el triángulo ACD solución del problema.

Discusión de la solución

En esta última solución puede verse fácilmente que el arco con centro A y radio a debe cortar al segmento MN, para lo que es necesario que se cumpla que La última igualdad se dará cuando AD sea la mediatriz de MN y el triángulo buscado sea isósceles.