De investigación

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 332. - Sea OAB con <O = 90º. Sean OM y ON las bisectrices interior y exterior de O, con M y N sobre la recta que contiene al lado AB. Sean M’ y N’ los pies de las perpendiculares trazadas por M y N, respectivamente, sobre la recta que contiene al lado OA. Consideremos los puntos siguientes:

X =M’N ∩MN’; Y =OM∩BM’; Z =N’B∩ON; U =BM’ ∩MN’ ; V =M’N ∩N’B; W =ON ∩AU;

S=M’N ∩OM; R=N’B ∩AS; T=N’M ∩ON; I=OM ∩AU; J=BM’ ∩AS

Probar que:

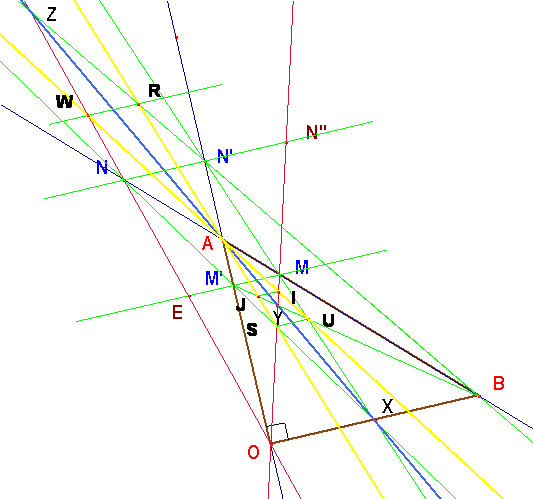
a) X, Y, Z, A son colineales, y están sobre la mediana del lado OB.

b) A, U, V, W son colineales

c) A, R, S, T, son colineales

d) US, I J, VT, y WR son paralelos a OB.

e) Los triángulos OMN, y M’BN’ tienen la misma área.

f) OB es la media armónica de MM’ y NN’.

Romero, J.B. (2006) : Comunicación personal.

Solución.-

a) Para demostrar la alineación de los puntos X, Y y Z bastará con considerar la proyectividad definida entre las rectas MN y M’N’ donde a la terna (M,N,B) le hacemos corresponder la terna (M’,N’,O). El eje de la misma está constituida por los puntos X, Y y Z. Se trata de una perspectividad, pues los pares de puntos homólogos (M,M’), (N,N’) y (O,B) definen rectas concurrentes en el punto del infinito del lado OB. De ahí que el punto común a MN’ y M’N, el punto A, sea fijo y por tanto pertenezca al eje proyectivo de la perspectividad. Con esto ya tenemos la alineación pedida.

Estos puntos están en la mediana del lado OB pues son los puntos de intersección de las proyecciones desde O y B de los puntos de corte con una paralela a ellos ( MM’ o NN’) según se ha probado en alguna ocasión anterior (ver problema nº 68).

En la figura no hemos tomado las bisectrices interior y exterior de O; es suficiente tomar una recta cualquiera por ese vértice y su simétrica respecto del cateto OA.

Para concluir esta parte demostraremos que el punto X es el punto medio de la base OB.

Los triángulos OMB y MNN” son homotéticos, con centro de homotecia M. Por la construcción realizada de las rectas OM y ON (y por ser recto AOB), N’ es el punto medio de NN”que indica que MN’ es la mediana de ese lado. El punto homotético de N’ está sobre esa recta y es el punto medio de OB.

Si ahora concluimos que también está sobre la recta M’N habremos probado ya que X es el punto medio de OB.

En efecto, en el triángulo ONB, M’ está en la mediana de OB pues es el punto medio del segmento EM paralelo a la base, por tanto NM’ es una mediana y corta a OB en su punto medio.

b, c y parte de d) Para seguir nuestra demostración debemos alterar el orden del enunciado. Vamos a probar antes una parte del apartado d).

Veamos que US, VT son paralelos a OB. En el primer caso tomo la proyectividad entre las rectas MN y M’N’ definida por (M,N,B) à (M’,O ,N’); se trata de la proyección desde el punto del infinito de OB de una sobre la otra . El eje de la misma está formado por los puntos U=M’B∩N’M ; S= M’N∩OM y P_inf= OB∩N’N.

En el segundo caso, la proyectividad se define por (M,N,B) à (O,N’,M’); en su eje yacen los puntos T=ON∩N’M ; V= M’N∩BN’ y P_inf= OB∩MM’.

Consideremos ahora la proyección desde A de las rectas anteriores. Se corresponden los pares (N,M) y (M’,N’). El punto común X es fijo. El eje de esta proyectividad pasa por el punto común a las dos rectas y por el punto P_inf= NN’∩MM’. Como hemos probado que X está sobre OB, resulta que el eje buscado es justamente esta recta.

Esta proyección puede interpretarse de otro modo. Dado un punto de la primera recta, por ejemplo N, la proyecto desde O en ON, tomo su simétrica OM respecto de OA y la corto con la segunda recta, MN’ obteniendo el punto M.

Este mismo proceso aplicado a M’ nos lleva al punto N’. Para el punto X considerado de M’N obtengo que su imagen es otra vez X pero en MN’, gracias a la alineación de X con OB como habíamos probado antes.

Con esta redefinición de la proyección desde A bastará con probar que las imágenes de los puntos S y V son los puntos T y U para tener asegurada su alineación con A.

Imagen de S: Uniendo S con M tengo la recta OM (según la definición de S), corto con el eje proyectivo OB en el punto O y proyecto éste último desde la antiimagen de M, el punto N. ON encuentra a la recta MN’ en T. Este será el homólogo de S.

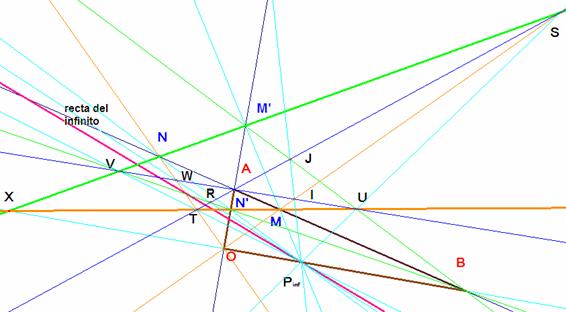
Imagen de V: El mismo procedimiento, lo proyecto desde N’ sobre el eje proyectivo en el punto B. Proyectándolo ahora desde la antiimagen M’ de N’ se obtiene el punto U sobre MN’. Es la imagen de V.

Con esto tenemos ya que A, U, V por una parte y A, S, T de otra son colineales. También W y R están en cada una de ellas por la propia definición de estos puntos.

d) Falta probar que IJ y WR son paralelos a OB.

Ahora consideramos una aplicación entre las rectas r_AS y r_AU. La imagen de la terna (R,S,T) de la primera es la terna (W,U,V) de la segunda.

El eje de esta homografía está definido por los puntos RV∩TW=BN’∩ON=Z; TU∩SV=MN’∩M’N=X. Se trata de la recta que contiene a los puntos A, X, Y y Z. Como el punto de intersección de r_AS y r_AU pertenece al eje, esta aplicación es una perspectividad y por tanto todos los pares homólogos concurren en un mismo punto P_inf donde ya hemos visto que concurren (U,S) y (V,T). Esto prueba que WR es paralelo a OB. Si la imagen de J es I habremos concluido.

Para calcular el homólogo de J haremos uso del eje proyectivo. La proyección sobre él desde U (UJ=BM’) lo lleva a Y. La proyección desde S (antiimagen de U) sobre r_AU nos da I=OM∩AU.

e) Los triángulos NOB y N’OB son equivalentes por tener igual base y altura. El primero de ellos contiene al triángulo OMB, equivalente por igual causa al triángulo OMB’ contenido en el segundo. En consecuencia los triángulos residuales OMB y OM’B han de ser equivalentes también.

f) Si tenemos una cuaterna armónica (P Q R S) = -1 es fácil demostrar que

(*)

puede verse, por ejemplo en la obra Geometría Métrica vol I, pág. 149 del profesor P. Puig Adam. Se dice en este caso que el segmento RS es la media armónica de los segmentos PS y QS.

Por el teorema de la bisectriz, las intersecciones de las bisectrices de un ángulo separan armónicamente a los vértices del lado opuesto, por tanto la razón doble de los puntos N, M, B y A es -1: (M,N,B,A)=-1, lo cual quiere decir que el segmento AB es media armónica de los segmentos MA y NA. Cuando se proyecta una razón doble ésta no varía, así pues, proyectando la cuaterna (M,N,B,A) sobre la recta NN’ desde el punto del infinito de la recta OA, el segmento AB se proyecta en OB, MA en M’M y NA en NN’ y por tanto, tenemos que el primero es la media armónica de los otros dos, como se pretendía probar.