Problema 333 de triánguloscabri

Solución de Francisco Javier García Capitán

Usaremos las coordenadas baricéntricas y el programa Mathematica para investigar el problema propuesto.

Definimos un punto D variable sobre la recta BC y usamos la función CuadradoDistancia para imponer a D que cumpla la propiedad requerida y obtener una expresión que deberá anularse:

El primer factor corresponde al punto D = {0,-b²,c²}. Teniendo en cuenta que {a²,b²,c²} son las coordenadas del punto simediano, AD será la recta conjugada armónica respecto de AB y AC de la simediana corrrespondiente a A. Sin embargo, el punto D en este caso es exterior al segmento BC, por lo que tendremos BD·DC < 0 y no será una solución del problema.

El segundo factor del numerador, por ser de segundo grado, corresponderá a dos puntos, uno o ninguno y podemos pensar que dichos puntos son la intersección con la recta BC y una circunferencia determinada. Comenzamos entonces por completar la expresión del segundo paréntesis con términos en x², xy y xz.

Queremos buscar una circunferencia sencilla de este tipo. Si obligamos a que la circunferencia pase por A, deberá ser p=0.

Hallemos los puntos de corte con los lados AB y AC.

Esto quiere decir que los puntos de corte con AB y AC son {-c², q,0} y {-b², 0,r} respectivamente. Si hacemos q = -c² y r = -b² los puntos de corte serán {1,1,0} y {1,0,1}, es decir, los puntos medios de los lados. La cónica que queda con estos valores es

Para comprobar que es una circunferencia hacemos:

Por tanto, para hallar los puntos D sobre BC tales que AD²=BD·DC basta hallar la intersección con BC de la circunferencia que pasa por el vertice A y los puntos medios de W y V de AB y AC, respectivamente.

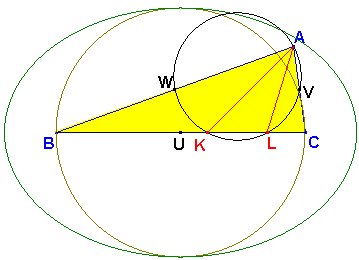En la figura adjunta hemos dibujado un triángulo ABC. Supongamos que el lado BC es fijo y que el punto A varía por el plano. Trazamos la elipse que tiene por focos a B y C, con eje menor midiendo lo mismo que BC, es decir con excentricidad igual a

Será dependiendo de que A esté en el interior de esta elipse, sobre esta elipse o fuera de esta elipse cuando existan dos puntos solución, los dos puntos se confundan en uno, o no existan respectivamente.

En la figura se ve el caso general de que hay dos soluciones K y L.

En el caso particular de que A esté sobre la circunferencia de diámetro BC (es decir, cuando ABC es rectángulo en A) , resultará que K coincidirá con el punto medio de BC y L será el pie de la altura trazada por A.