De investigación

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

De investigación

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 333.- Sea  d = AD,  una ceviana del triángulo ABC, tal que d²= mn, donde m =BD, y n=DC

Caracterizar si existen o no triángulos distintos de los triángulos rectángulos que verifiquen la propiedad anterior.

Nota. A m, y, n, que verifican a=m+n, se les puede llamar la proyección paralela de los lados AC, y AB, sobre la ceviana AD (como base del paralelismo)

Romero, J.B. (2006): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Supongamos que tenemos unos ejes coordenados donde situamos el triángulo tal como se indica en la figura. Hemos tomado la longitud de BC como unidad, para simplificar los cálculos, pero esencialmente no se modifica nada si se pone un valor arbitrario a.

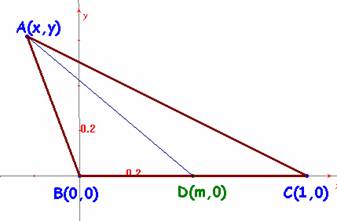
La expresión del módulo de AD es |AD|² = d² = (x-m)²+ y². Y la condición del enunciado, teniendo en cuenta que n=1-m es

m(1–m) = (x–m)² + y²   (1)

Desarrollando y agrupando en m nos queda:

2m² – (2x+1)m + (x² +  y²) = 0   (2)

Para que esta ecuación tenga soluciones en m ha de tener discriminante no negativo, esto es, se debe verificar la inecuación

(2x+1)² –8(x² +  y²) ≥ 0       (3)

o de forma equivalente, efectuando los cálculos precisos

(2x–1)² +8y² ≤ 2      (4)

que también puede ponerse como 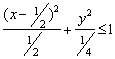                      (5).   

En resumen, el punto A(x, y) debe elegirse dentro de esa elipse con centro en el punto medio del lado BC y semiejes respectivos  y 1/2.

Los valores extremos de la x, se obtienen para y=0, son , de ahí que el coeficiente 2x + 1  de la ecuación (2) sea siempre positivo, ya que su valor mínimo es 2 – . Con eso podemos asegurar que, si esta ecuación tiene soluciones, éstas son positivas: habrá dos cevianas AD solución del problema. La y podemos considerarla siempre positiva (los valores opuestos darán soluciones simétricas respecto al eje de abscisas) moviéndose entre 0 y ½ .

Los triángulos rectángulos en A siempre cumplen la condición del enunciado, para ellos, este vértice ha de estar sobre la circunferencia de diámetro BC. La condición se expresa por la ecuación

x² + y² = x        (6)

También hay dos cevianas solución, corresponden a los valores de m=x (la altura sobre la hipotenusa) y  m=1/2 (la mediana sobre BC).

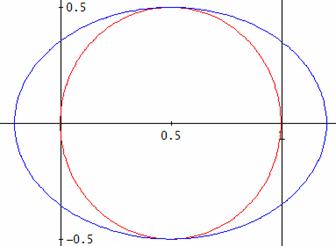
La segunda figura representa la elipse de la expresión (5)  en color azul y la circunferencia de la expresión (6) en rojo.

Siempre que el punto A se mueva en el interior de esa elipse –en particular si se mueve sobre la circunferencia roja, totalmente dentro de la elipse– la ceviana AD cumplirá la condición buscada, pues entonces la ecuación  (2) en la incógnita m tendrá siempre dos soluciones positivas. Su discriminante es positivo y la sucesión alternada de coeficientes es + - +, que asegura que las soluciones son positivas.

            Hay triángulos solución que no son rectángulos en A, pero sí lo son en B o en C, siempre que el vértice A se tome sobre la porción de las rectas x =0 o x=1 que está dentro de la elipse.

Para calcular un triángulo concreto de los buscados, tomemos, por ejemplo, x= 3/4 e y = ¼, valores que cumplen las condiciones exigidas.

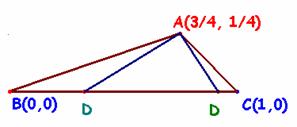
La ecuación en m correspondiente es 2m² – 5/2m + 5/8 = 0 y sus soluciones m = . El punto D=(,0)  AD=(, -1/4) y |AD|² = d² =1/64=. De otra parte n= y el producto mn=·= con un poco de paciencia para hacer los cálculos. Su aspecto es muy parecido al de la figura.