De investigación

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 333

       Sea  d = AD,  una ceviana del tríangulo ABC, tal que d^2= mn, donde m=BD, y n=DC.

         Caracterizar si existen o no triángulos distintos de los triángulos rectángulos que verifiquen la propiedad anterior.

Nota. A m, y, n, que verifican a=m+n, se les puede llamar la proyección paralela de los lados AB, y AC, sobre la ceviana AD(como base del paralelismo)

Romero, J.B. (2006): Comunicación personal.

Solución de Mark Tudosi.

Señala Mark que son para él notas sobre el poblema

Hay pares de soluciones algebraicas, observemos las geométricas.

La expresión AD^2 = BD * DC es una expresión para una media geométricamedio de BD y DC.

Así, tenemos que construir un semicírculo con BC como diámetro y hacer la perpendicular a BC por el punto D hasta la intersección con el semicírculo.

Este valor tiene que ser igual a la ceviana AD, así que una posición sobre BC tiene que ser encontrada de tal manera que la circunferencia con el radio la media geométrica tiene que pasar por el vértice A.

Es obvio que hay 2 posiciones cuando sucede y que sucede solamente si el ángulo A no es agudo.

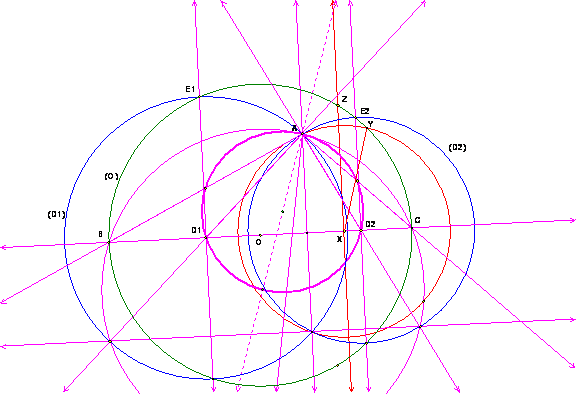
Del esquema es obvio quelos ángulos BAD1 y CAD2 deben ser iguales por consideraciones de simetría (véase el círculo rojo que no cumple el requisito), pero yo conjeturo una demostración más fuerte para establecer este hecho.

Una vez que se haga, lo que sigue es el hecho de que hay una circunferencia tangente al circuncírculo de ABC en el vértice A, que es homotética con el centro A y el factor 1/2 del mismo circuncirculo.

Los puntos D1 y D2 son centros de los círculos azules con los diámetros que son cuerdas de ABC del círculo que empiezan en A.

Así esta circunferencia homotética (la púrpura en el esquema) pasará por tantopor los puntos medios de los lados AB y CA e intersecará a BC en los puntos requeridos D1 y D2

También miraba la fórmula de Stewart para AD^2. Después de algo directo los pasos me llevaron a una ecuación cuadrática para BD, y es quizá fácil ver cuál señala D1 y D2 que son las expresiones de las raíces, pero no soy bueno en álgebra.

También debe habar claramente condiciones cuando no hay raíces reales, y cuando hay una solamente. Si eres bueno en álgebra quizá este análisis es de mérito y se debe hacer apenas para acabar de este problema.

There are a couple of algebra solutions, my note about the geometry of it.

The expression AD ^ 2 = BD * DC  is an expression for a geometric

mean of BD and DC. 

Thus, we have to construct a semicircle on BC  as diameter and make perpendicular to BC at point D to intersection with the semicircle.

This value has to be equal to cevian AD, so a position  on BC has to be found such that  the semi circle  with radius of geometric mean  has to pass  through vertex A .

It is obvious that there are 2 positions when it happens and that it happens only if the angle A is not acute.

 From the  sketch it is obvious that the angles BAD1  and CAD2 are

equal from symmetry considerations (see red circle that does not fit the requirement ) , but I guess a stronger proof needed  to establish this fact.  

Once it is done, what follows is the fact that there  is a circle tangent to circumcircle of ABC at vertex A. that sets up a  homothety with center A and factor  1/2  that takes every chord starting at A

and maps it's midpoint to the circumcircle.

Points D1 and D2  are centers of the blue circles with diameters being the chords of circle ABC starting at A. 

So this homothety circle ( the purple one on the sketch ) will pass

through midpoints of the sides AB and AC and intersect BC in the required points D1 and D2 ( will take D1 and D2 ant map to intersection points of circumcircle and  the circles of radius equal to the geometric mean of BD and DC, the blue ones on the sketch).

I also looked at Stewart formula for AD^2. After some straightforward

steps it gave a quadratic equation for BD, and maybe it is easy to see

what points D1 and D2 are from the roots expressions, but I am not good at algebra.

It also should make clear the conditions when there are no  real roots, and when there is one only. If you are good at algebra maybe this analysis is worthwhile and should be done just to finish off this problem.