Propuesta de Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priego de Córdoba)
Problema 334
Sean ABC un triángulo y H su ortocentro.
Demostrar que si A', B', C' son los circuncentros de los triángulos HBC, HCA y HCB, entonces el triángulo A'B'C' es congruente con ABC.
García, F.J. (2006): Comunicación personal
Solución del director.
Sea ABC el triángulo dado y H su ortocentro
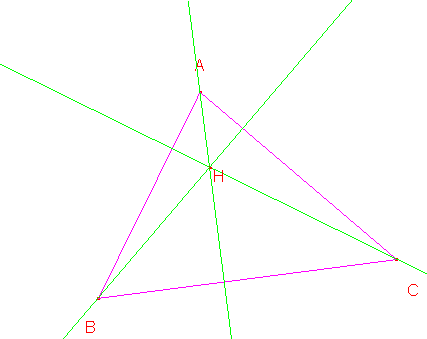
Construyamos el punto A’:
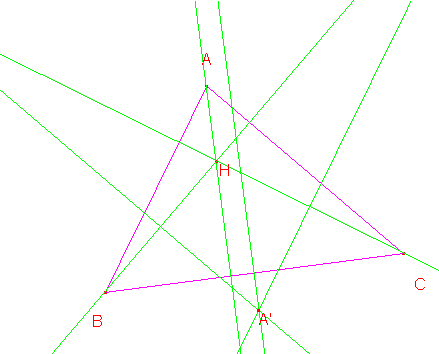
Será el punto de encuentro de las mediatrices de BC, BH y CH.
Construyamos ahora B’ y C’ de igual manera.
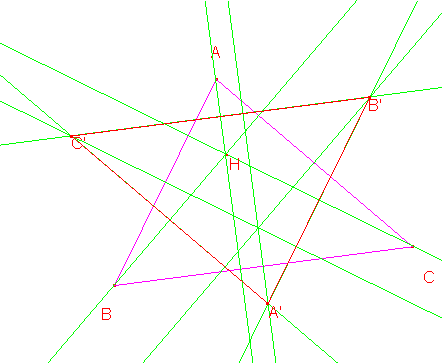
Tenemos que AH es lado común de AHC y AHB, luego estos dos triángulos tienen la misma mediatriz respecto a AH y así el lado B’C’ está sobre tal mediatriz, que por ser AH perpendicular a BC, tiene como consecuencia que B’C’ es paralelo a BC.
Igual consecuencia, lógicamente para A’B’ y C’A’.
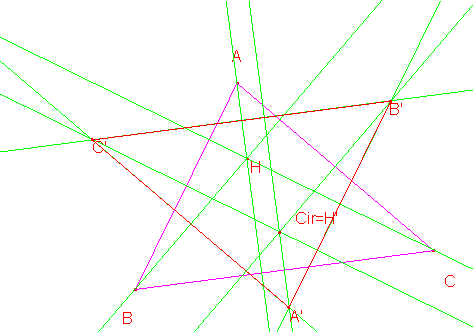
Las tres mediatrices de AB, AC y BC que se cortan en Cir, el circuncentro del triángulo ABC, pasan a ser pues, las alturas del triángulo A’B’C’ que se cortan en H’=Cir.
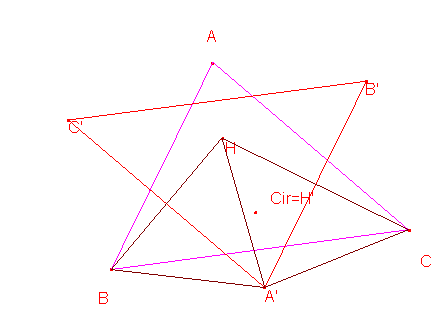
Consideremos los triángulos A’CH y A’BH.
Ambos son isósceles pues A’ es el circuncentro de BHC y A’B=A’H=A’C.
Al ser CH perpendicular a AB, es <BCH=90-B.
Al ser BH perpendicular a AC, es <CBH=90-C.
Por ello, además, es <BHC=180-(90-B)-(90-C)=B+C
Al ser el ángulo mayor < BA’C el ángulo central del <BHC, es <BA’C=2B +
Así el ángulo menor <BA’C=2A, y dado que también el triángulo A’BC es isósceles, tenemos que <BCA’ = <CBA’ =90-A.
De esta manera tenemos que < HBA’ = < HBC + < CBA’ = (90-C)+(90-A)=B.
Al ser el triángulo HBA’ isósceles, es <BHA’=B, y < BA’H =180-2B.
En el triángulo A’HC, de manera análoga, es <A’HC = <A’CH = C, <CA’H= 180 -
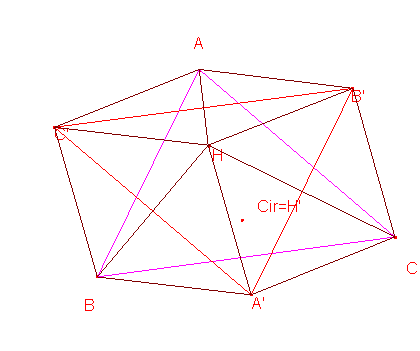
Completando los demás, tenemos, por ejemplo, que:
<C’HB =<C’BH=B, <B, <BC’H=180-
De esta manera, los triángulos BHA’ y BHC’ son simétricos respecto a BH.
Así, BC’ = BA’.
Por analogía tenemos, alternado las razones de isósceles y simetría, que
BA’=A’C = CB’= B’A =AC’ = C’B.
Además se tiene también que A’H=B’H=C’H, por lo que H es el circuncentro de A’B’C’.
Ahora, consideremos por ejemplo los triángulos isósceles A’BC y AB’C’.
Tienen los lados iguales con el mismo valor, A’B=A’C=AC’=AB’.
El ángulo desigual coincide: BA’C=C’AB’=2A. De ello, C’B’=BC.
Por motivos análogos, A’B’ = AB y A’C’ = AC.
De todo ello, se llega a lo requerido por el problema, los triángulos ABC y A’B’C’ son congruentes.
Estos dos triángulos intercambian el ortocentro y el circuncentro.
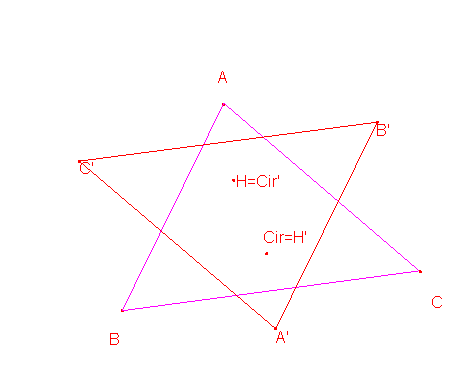
Ricardo Barroso Campos.
Didáctica de las Matemáticas.
Universidad de Sevilla.