Problema 334 de triánguloscabri

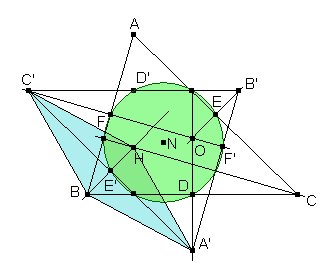
Sean ABC un triángulo y H su ortocentro. Demostrar que si A', B', C' son los circuncentros de los triángulos HBC, HCA y HCB, entonces el triángulo A'B'C' es homotético a ABC.
Propuesto por Francisco Javier García Capitán

Solución de Francisco Javier García Capitán

Recordemos que la circunferencia de los nueve puntos del triángulo ABC pasa por los puntos medios de los lados BC, CA, AB, los pies de las alturas y los puntos medios de los segmentos que unen el ortocentro con cada uno de los vértices.

También que el centro N de esta circunferencia es el punto medio del circuncentro O y ortocentro H.

Olvidemos por el momento la definición de A', B', C' que da el enunciado y consideremos la simetría central de centro N, y llamemos en general P' a la imagen de P por esta transformación.

Demostraremos que A' es el circuncentro del triángulo HBC, que es la definición del enunciado.

  1. Por ser N el punto medio de H y O es H' = O y O' =H, resultando, mediante la transformación, que H y O son el circuncentro y ortocentro, respectivamente del triángulo A'B'C'.
  2. Los triángulos ABC y A'B'C', con el circuncentro y ortocentro intercambiados comparten la misma circunferencia de los nueve puntos.
  3. El punto medio E de CA se transforma en el punto medio E' de C'A'. Como OE es perpendicular a CA, su transformada HE' es perpendicular a C'A' y también a CA, ya que CA y C'A' son pralelas. Entonces HE' es la altura trazada por B y el punto E', al estar en dicha altura y en la circunferencia de los nueve puntos de ABC, debe ser el punto medio de BH.
  4. Entonces A'HC'B es un rombo y, lo que nos interesa, A'B = A'H. De la misma forma se demostraría que A'C = A'H, por lo que A' es el circuncentro del triángulo HBC.