Propuesta de Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priego de Córdoba).

Problema 334.- Sean ABC un triángulo y H su ortocentro.

Demostrar que si A', B', C' son los circuncentros de los triángulos HBC, HCA y HAB, entonces el triángulo A'B'C' es congruente con ABC.

García, F.J. (2006): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

La recta h_a (altura desde A) es el eje radical de las circunferencias de centros B’ y C’ y por ello perpendicular a B’C’. En consecuencia B’C’ es paralela a BC. Análagamente los demás lados. Ya tenemos que los triángulos ABC y A’B’C’ son homotéticos (en posición de Thales).

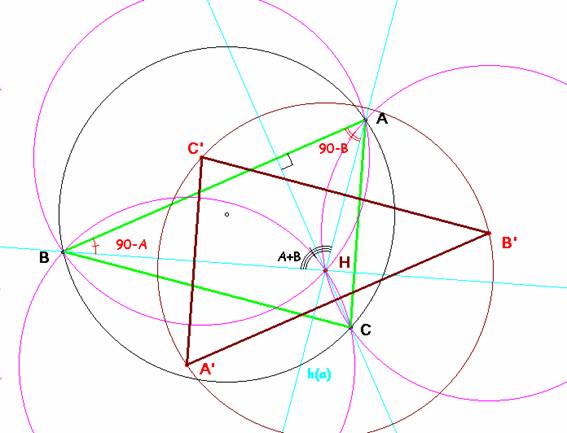
Si ahora aplicamos el teorema de los senos al triángulo BHA en la circunferencia de centro C’, el diámetro de ésta es el cociente = == diámetro de la circ. circunscrita al triángulo ABC. Lo mismo sucede con las circunferencias de centros A’ y B’.

En consecuencia, si AC’ = AB’  el punto A está en la mediatriz de B’C’ y las alturas del triángulo ABC  son mediatrices de A’B’C’ y por tanto, el ortocentro del primero H,  es el circuncentro del segundo.

De otra parte, HB’=AB’(son radios de la misma circunferencia) lo que nos dice que la circunferencia circunscrita a A’B’C’ también tiene radio R, como las demás.

La conclusión es inmediata: si los triángulos de lados paralelos ABC y A’B’C’ tienen circunferencias circunscritas de igual radio es porque son congruentes como se quería demostrar.