Art of Problem Solving, incluyendo algunas aclaraciones que el autor me ha hecho llegar mediante el correo electrónico.)
Primera parte: Los puntos isodinámicos son inversos respecto de la circunferencia circunscrita
|
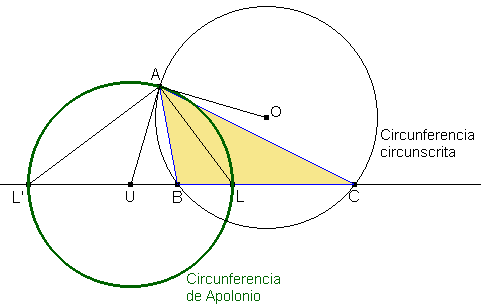
Lema 1. En un triángulo cada circunferencia de Apolonio es ortogonal a la circunferencia circunscrita. Demostración. Consideremos la circunferencia de Apolonio correspondiente al vértice A. Esta circunferencia tiene diámetro LL', siendo L y L' las intersecciones con BC de las bisectrices del ángulo A. Sean O el centro de la circunferencia circunscrita y U el centro de la circunferencia de Apolonio correspondiente a A.
|
Los puntos isodinámicos son los puntos de intersección de las tres circunferencias de Apolonio del triángulo. Como cada una de estas circunferencias es ortogonal a la circunferencia circunscrita, resulta que cada circunferencia de Apolonio es fija mediante la inversión respecto de la circunferencia circunscrita. Uno de los puntos isodinámicos que está en las tres circunferencias, debe aplicarse en el otro.
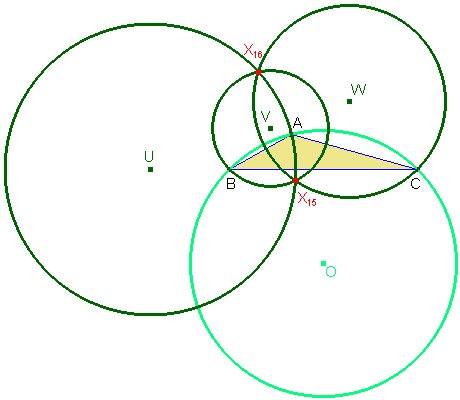
Segunda parte: Los puntos isodinamicos dividen armónicamente al diámetro de Brocard.
|
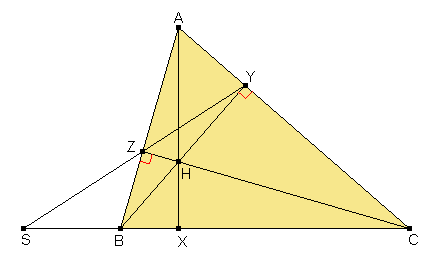
Demostración. Como las alturas AX, BY, CZ se cortan en el ortocentro H, el teorema de Ceva nos dice que Por otro lado, como la transversal YZ corta a BC, CA, AB en S, Y, Z, respectivamente, el teorema de Menelao nos dice que Comparando las dos igualdades resulta
|
|
Demostración. Por ser AB la polar del punto S respecto de la circunferencia con diámetro EF se cumple que (EFS'S) = -1. Supongamos que EC y FD se cortan en X. Como EC^CF y FD^ED, aplicando el aplicando el corolario del Lema 2 resultará que EC, FD y AB son concurrentes en X. Ahora, proyectando la recta EF sobre la recta CD desde el punto X obtenemos que (CDTS) = (EFS'S) = -1. |
Pasemos ya a demostrar que los puntos isodinámicos dividen armónicamente al diámetro de Brocard. Tenemos:
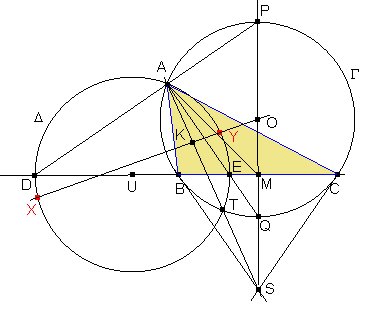 G
es la circunferencia circunscrita a ABC, con centro O.
G
es la circunferencia circunscrita a ABC, con centro O.
- M es el punto medio del lado BC.
- La bisectriz exterior del ángulo A corta en D a la recta BC y en P a G.
- Las bisectriz interior del ángulo A corta en E a la recta BC y en Q a G.
- U es el punto medio de DE.
- La circunferencia D con centro U y diámetro DE se llama circunferencia de Apolonio de ABC correspondiente a A.
- Las tangentes a G en B y C se cortan en S.
- T es el otro punto de intersección de G y la circunferencia de Apolonio correspondiente a A.
A partir de aquí,
- PQ es un diámetro y la recta PQ pasa por S.
- La cuaterna (PQMS) es armónica y el ángulo ÐPAQ es recto. En consecuencia, AP y AQ son las bisectrices del triángulo MAS, y AS es la simediana correspondiente a A del triángulo ABC.
- La polar de S respecto de la circunferencia G , que es BC, pasa por U. En consecuencia, la polar de U respecto de G a su vez pasará por S. Pero la polar de U respecto de G es la recta AT, ya que las circunferencias D y G son ortogonales. Por tanto, T, A y S están alineados.
- La simediana del triángulo ABC correspondiente a A es el eje radical de D y G.
- Considerando la circunferencia G y dos de las circunferencias de Apolonio, el centro radical de las tres circunferencias será el punto de intersección de las dos simedianas correspondientes, es decir, el punto simediano K. El eje radical de dos de las circunferencias de Apolonio es la recta que une los puntos isogonales y el punto K está en dicha recta. Los puntos isogonales, por tanto, están en la recta OK.
- Finalmente, teniendo en cuenta que AT es la polar de O respecto de D, llamando X e Y a los puntos isodinámicos, y usando el Lema 3 tendremos que (XYKO) = -1.
 Lema
2. Sean X,Y,Z los pies de las alturas desde
A, B, C sobre BC, AC, CA
en el triángulo ABC. Si YZ corta a BC
en S, entonces (BCXS) = -1.
Lema
2. Sean X,Y,Z los pies de las alturas desde
A, B, C sobre BC, AC, CA
en el triángulo ABC. Si YZ corta a BC
en S, entonces (BCXS) = -1.
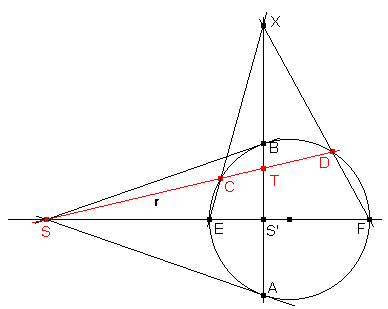 Lema
3 . Sean EF un diámetro de una circunferencia
y S un punto exterior a la circunferencia que está
en la recta EF. Supongamos que las tangentes desde S
a la circunferencia tocan a la circunferencia en A, B
y sea S' = AB Ç
EF. Sea r una recta cualquiera que pasa por S,
corta en C, D a la circunferencia y en T al
semgento AB. Entonces (CDTS) = -1.
Lema
3 . Sean EF un diámetro de una circunferencia
y S un punto exterior a la circunferencia que está
en la recta EF. Supongamos que las tangentes desde S
a la circunferencia tocan a la circunferencia en A, B
y sea S' = AB Ç
EF. Sea r una recta cualquiera que pasa por S,
corta en C, D a la circunferencia y en T al
semgento AB. Entonces (CDTS) = -1.