De
investigación
Propuesto
por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de
Valladolid
Problema 337 .- Si ABC es un triángulo
obtusángulo en A, r, radio del círculo
inscrito, R, radio del círculo circunscrito al triángulo, a, su lado mayor
y p el perímetro respectivamente, probar que :
![]()
¿Cúando se alcanza la igualdad?
Romero, J.B. (2006): Comunicación personal
Demostración
a)
Para la primera desigualdad la idea de la demostración es tratar de encontrar
los triángulos para los cuales la razón de los radios alcanza el valor máximo,
si es que existen, y probar la desigualdad en ese caso.

Es fácil ver que, situando A sobre el arco capaz de BC y amplitud el ángulo BAC, la altura sobre BC varía alcanzando el valor máximo
cuando el triángulo es isósceles. Al mismo tiempo, el radio de la
circunferencia inscrita varía también en el mismo sentido, manteniéndose
siempre inferior a la altura. La intuición nos dice que este radio será máximo
cuando lo sea aquella. Y en efecto así es. En el problema nº 285 demostramos
que “el lugar geométrico del incentro de
un triángulo con dos vértices fijos B y C y el otro A variable sobre un arco de
circunferencia es otro arco de circunferencia que pasa por los puntos fijos y
que tiene su centro en el punto medio P del arco BC que no tiene al otro
vértice ”. por todo esto, resulta que IM
es el radio máximo.
Para concluir esta primera parte
debemos demostrar la desigualdad en este caso particular (el de radio máximo).
De la fórmula del área del triángulo se obtiene p·r=a·h
siendo h la altura sobre el lado
mayor a. Despejando se tiene
r=a·![]() (1)
(1)
Utilizando el teorema de los senos encontramos para
los lados del triángulo las siguientes igualdades: b=2R·sen B; c=2R·sen C ; a=2R·sen A y por último h=c·sen
B.
Llevando todo esto a (1) resulta
![]() (2)
(2)
En la fórmula (2)
sustituimos los ángulos B y C por sus valores: B=C=90-A/2. Obtenemos:
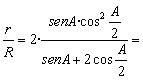
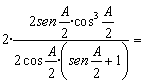
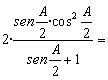
=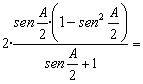
![]()
Llamando x= sen (A/2), tenemos que resolver la inecuación
2x(1—x) ≤ ![]()
o bien
2x2 – 2x +(![]() )
)![]() 0. (3)
0. (3)
La ecuación asociada tiene como soluciones ![]() , por tanto, las soluciones de la inecuación son los números
reales que se encuentran fuera del intervalo
, por tanto, las soluciones de la inecuación son los números
reales que se encuentran fuera del intervalo 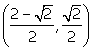 . Si x=sen(A/2), cuando el ángulo A no
es agudo, esto es, 45º<A/2<90º, se tiene que
. Si x=sen(A/2), cuando el ángulo A no
es agudo, esto es, 45º<A/2<90º, se tiene que ![]() , y por tanto sen(A/2) es solución de la inecuación,
como queríamos probar.
, y por tanto sen(A/2) es solución de la inecuación,
como queríamos probar.
La igualdad se da cuando ![]() =sen(A/2), que se cumple para un triángulo,
únicamente cuando el ángulo A es recto:
así r/R = 2·sen 45º(1-
sen 45º)=
=sen(A/2), que se cumple para un triángulo,
únicamente cuando el ángulo A es recto:
así r/R = 2·sen 45º(1-
sen 45º)=![]() .
.
b) Para demostrar la segunda desigualdad![]() , previamente vamos a transformarla en otra equivalente más sencilla.
, previamente vamos a transformarla en otra equivalente más sencilla.
Si esta es cierta, pasando el 1 al segundo miembro y elevando al cuadrado resultan:
2p2 ≤
a2 + 2a·p + p2
p2 ≤ a2
+ 2a·p
(a+b+c)2 ≤
a2 +2a·(a+b+c)
(b+c)2
≤ 2a2
Utilizando
ahora el teorema del coseno a2
= b2 + c2 -2bc·cos A podemos poner
2·bc
(1+cos A) ≤ a2. (4)
Esta desigualdad es equivalente a la
queremos demostrar. Previamente necesitamos un resultado:
Si el ángulo en A no es agudo, 1+ cos A ≤ sen A.
sen A – cos A = sen A – sen(90–A)= 2·cos45·sen(A–45)=![]() ·sen
(A–45)≥1. Para que esto se verifique
ha de ser 45º≤ A–45º ≤ 135º, o
sea, que el ángulo A no sea agudo.
·sen
(A–45)≥1. Para que esto se verifique
ha de ser 45º≤ A–45º ≤ 135º, o
sea, que el ángulo A no sea agudo.
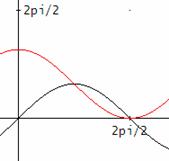
Gráficamente podemos verlo sin más que representar las funciones y=sen
x (en negro) e y=1+ cos x (en rojo). La primera tiene
su gráfica por encima de la segunda entre p/2 y p.
La desigualdad (4) implica esta otra
2·bc sen A ≤
a2. (5)
A ésta última puede dársele un significado geométrico. El primer
miembro es igual a cuatro veces el área del triángulo.
4.Área(ABC)
≤ a2 (6)
En el problema 270 demostramos que
para un triángulo con un ángulo A no agudo se verifica que a2 =4R·ma donde ma es la
mediana relativa al lado([1]) a.
Se tiene ahora
4.Área(ABC)
=2.aha≤ 2.ama ≤ 4R·ma=
a2 (pues
a ≤2R)
y
con ello concluimos la demostración de la desigualdad.
La desigualdad 1+ cos A ≤ sen A utilizada en la demostración es
una igualdad cuando el ángulo A es
recto. Podemos esperar que entonces la desigualdad demostrada sea también una
igualdad, pero no es así. Si tomamos un triángulo rectángulo cuyos ángulos
agudos midan, por ejemplo, 30 y 60 grados respectivamente, sus lados son a, a/2 y ![]() .
.
La relación entre la hipotenusa y el perímetro es
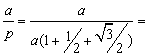
![]()
![]() .
.
Es en el triángulo rectángulo isósceles donde se alcanza la igualdad.
En
este caso b = c = ![]() y
y 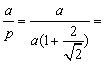
![]() .
.