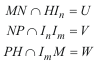Problema 341

En todo triángulo inscrito en una hipérbola equilátera, el punto de intersección de las alturas está situado sobre la curva.

Brianchon y Poncelet, Annales de Montpellier, Tomo XI, 1 de Enero de 1821.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de octubre de 2006)

DISCUSIÓN

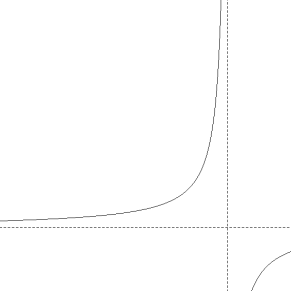
Sabemos que una hipérbola equilátera es un hipérbola cuyas asíntotas son perpendiculares.

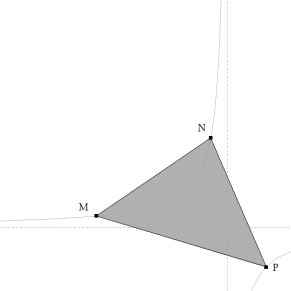
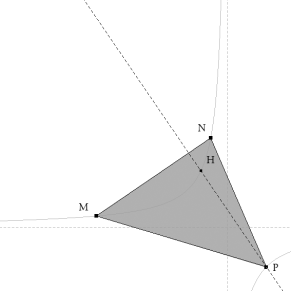
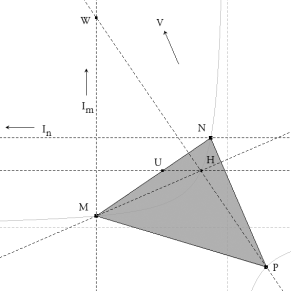
Sea MNP un triángulo inscrito en la curva.

Si trazamos la altura desde uno de los vértices, por ejemplo desde el vértice P, esta altura vuelve a encontrar a la hipérbola en un punto H.

Vamos a demostrar que H es el ortocentro del triángulo MNP y para ello demostraremos que MH es perpendicular a NP.

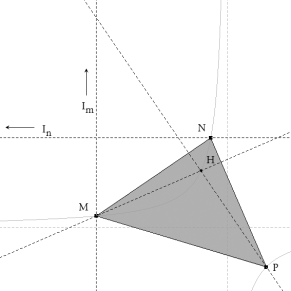
Tracemos por el primer vértice M una paralela a una asíntota y designemos el punto del infinito de esta paralela como I_m. Tracemos por el segundo vértice N una paralela a la otra asíntota y designemos el punto del infinito de esta paralela como I_n.

Por la propia definición de hipérbola, cónica con dos puntos en la recta del infinito; por la definición de asíntotas, tangentes en los puntos del infinito; y las paralelas con las asíntotas, tienen los puntos del infinito en común; podemos decir que I_m e I_n pertenecen a la hipérbola y son además sus dos puntos del infinito.

Damos por conocido el Teorema de Pascal, que aplicamos al hexágono inscrito MNPHI_nI_m, y tenemos en cuenta que el lado del hexágono HI_n es paralelo a NI_n y que el lado I_nI_m es la recta del infinito.

Por el teorema, podemos asegurar que U, V, W están en línea recta. Es decir, la recta UV es paralela a NP.

Pero la recta UW es perpendicular a MH, ya que MU, HU son dos alturas del triángulo MWH; entonces MH es perpendicular a NP, y el resultado queda demostrado.