Problema 341.- En todo triángulo inscrito en una hipérbola equilátera, el punto de intersección de las alturas está situado sobre la curva.

Brianchon y Poncelet, /1821) Annales de Montpellier, Tomo XI, 1 de Enero. 

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.-

Para resolver el problema necesitamos previamente algunas definiciones y resultados de Geometría Proyectiva .

Involuciones.- Son proyectividades de una recta en sí misma donde dos elementos A, A’ se corresponden doblemente, (que la imagen de A’ sea otra vez A). De ser esto así se corresponden doblemente los restantes puntos homólogos.

De los pares (A, A’) y (A’, A) se dice que son recíprocos en la involución.

Involución absoluta o cíclica. - Se llama así a la definida en la recta del infinito por los puntos de corte de los pares de rectas perpendiculares. Es, evidentemente, una involución elíptica (sin puntos fijos).

1.- El teorema del cuadrivértice de Desargues

a) Los tres pares de lados opuestos de un cuadrivértice PQRS son cortados por cualquier línea r que no pasa por ningún vértice en tres pares recíprocos de una involución entre puntos de r (forma débil).

b) Dada una cónica y un cuadrivértice inscrito en ella, toda recta r que sea secante a la cónica, sin pasar por ninguno de los vértices del cuadrivértice, corta a la cónica y a los lados opuestos del cuadrivértice en pares de puntos homólogos en una misma involución (forma fuerte).

Demostración

Bastará demostrar, por ejemplo, que (ABB’C’) = (A’B’BC). En efecto: proyectando la primera desde S sobre PR y posteriormente sobre r desde Q, resultan:

(ABB’C’) =(PB”B’R)=(CBB’A’) y en esta última permutando primero y último y los otros dos, (CBB’A’) = (A’B’BC).

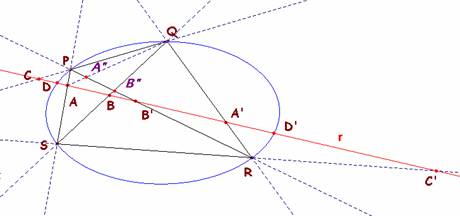
b) Consideremos la cónica generada por haces de vértices los puntos P y R. Tenemos la igualdad entre las cuaternas (PD PS PQ PD’ ) y (RD RS RQ RD’ ). Proyectando ambas sobre la recta r, se tiene que (DACD’) = (DC’A’D’) = (D’A’C’D) sin más que permutar dos pares de puntos. La igualdad entre la primera y la última cuaterna indica que en la proyectividad en la que son homólogos AA’, CC’ DD’ se corresponden doblemente D y D’, es decir, se trata de una involución.

Si consideramos la cónica generada por haces de rectas de vértices los puntos P y S, proyectando sobre la recta obtendríamos (DB’CD’) = (DC’BD’) = (D’BC’D) mostrando que B y B’ también se corresponden doblemente.

2.- Haces de cónicas.

Todas las cónicas que pasan por los cuatro vértices PQRS de un cuadrivértice constituyen un haz. Los pares de lados opuestos también se consideran cónicas del haz: son las cónicas degeneradas del mismo.

Del teorema de Desargues se desprende que los pares de puntos de intersección de una recta r que no pasa por ningún vértice con las cónicas de un haz pertenecen a una misma involución: la determinada sobre la recta por los pares de lados opuestos del cuadrivértice.

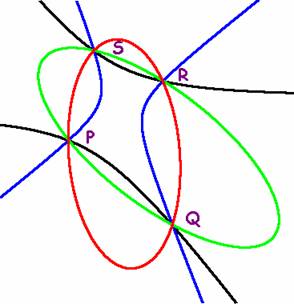
3.- Teorema.- Todas las cónicas que pasan por los puntos del cuadrivértice definido por un triángulo y su ortocentro son hipérbolas equiláteras.

Demostración

Las cónicas degeneradas del haz son pares de rectas perpendiculares (base y altura del triángulo), es decir, hipérbolas equiláteras. La involución inducida por el haz en la recta del infinito posee pues tres pares comunes con la involución absoluta (bastaría que fueran dos), en consecuencia, todos los pares de esta involución coinciden con la absoluta, o lo que es igual, todas las cónicas del haz son hipérbolas equiláteras.

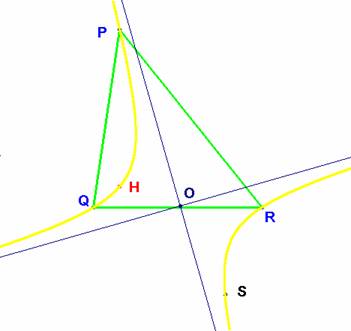
Solución del problema.

Sea PQR el triángulo inscrito en la cónica G y H su ortocentro. Supongamos que el ortocentro no está en la cónica. Tomo otro punto S cualquiera de la cónica y considero el haz de cónicas que pasan por los cuatro puntos. En este haz hay dos hipérbolas equiláteras: una la propia cónica G y otra la cónica del haz que pasa por el ortocentro H. En consecuencia todas las cónicas del haz son hipérbolas equiláteras.

Las cónicas degeneradas del haz (pares de rectas) también son hipérbolas equiláteras, o sea, son rectas perpendiculares y son las siguientes:

El par PQ, RS; el par PR y QS y el par QR y PS. Eso significa que el punto S (y cualquier otro punto de la hipérbola equilátera) es el ortocentro del triángulo PQR, y no H en contradicción con la hipótesis, luego no puede ser que H no esté en G.

El problema proporciona un procedimiento muy sencillo para dibujar hipérbolas equiláteras: se toma un triángulo y su ortocentro y otro punto más. La cónica que contiene a esos puntos es siempre una hipérbola equilátera.

Solución analítica del problema

Si se toman las asíntotas de la hipérbola como ejes de coordenadas, podemos suponer que la ecuación de la hipérbola equilátera es

xy = 1.

El triángulo tiene coordenadas P(p, 1/p); Q(q, 1/q) y R(r, 1/r). Vamos a calcular las coordenadas del ortocentro de este triángulo:

La ecuación de la altura desde R es: (x—r)(q—p)+ (1/q —1/p )( y—1/r)=0 y la de altura desde Q: (x—q)( r—p)+ (1/r —1/p )( y—1/q)=0.

Desarrollando estas ecuaciones se tienen:

(q—p) x + (1/q—1/p ) y = r(q—p) + 1/r (1/q —1/p )

(r—p) y + (1/r —1/p ) y = q(r—p) + 1/q (1/r —1/p )

La solución del sistema es el ortocentro. Resolviendo por la regla de Cramer resulta:

= == =

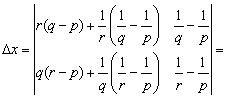
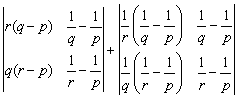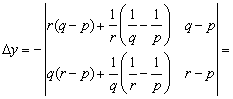
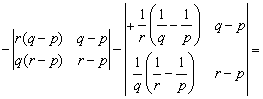
=(q—p)· (r—p)· (q—r).

Por último .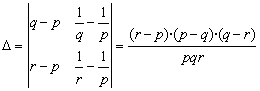

Las coordenadas del ortocentro son x = y y = —pqr que, evidentemente está sobre la hipérbola, pues verifican la ecuación xy = 1.

Que el lector escoja la solución que más le guste.