Problema 342.- Sean A', B' y C' , A'', B'' y C'' los pies de dos ternas de cevianas de un triángulo ABC concurrentes en P' y P'' respectivamente. Entonces los puntos A', B', C', A'', B'', y C'' yacen en una cónica. Recíprocamente: Se tiene un triángulo ABC que corta a una cónica en puntos A' B' C' A'' B'' C'' de suerte que sean concurrentes AA' BB' CC' en P'. Entonces las rectas AA'' BB'' CC'' también son concurrentes.

Campo, S. (2005) Métodos sintéticos de la geometría. Edición de autor. Salamanca. (p.184)

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Consideremos la proyectividad entre el lado AB y el lado AC definida haciendo corresponder a la terna (B, C’, C”) de AB la terna (C, B’, B”) de AC.

El eje de esta proyectividad es la recta definida por P’=BB’ÇCC’, P”=BB” ÇCC”. Además la recta P’P” contiene el punto A* =B’C” ÇB”C’.

Considerando proyectividades análogas entre los otros pares de lados del triángulo llegamos a la conclusión de que la recta P’P”, eje de cada una de ellas, contiene a los puntos A*, B*=A’C”ÇA”C’ y C*=A’B”ÇA”B’.

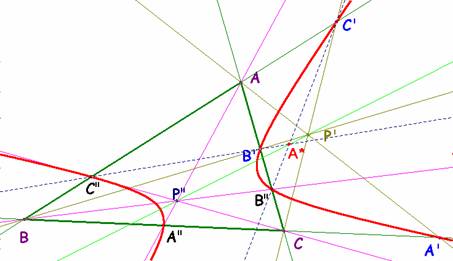
Si considero ahora el hexágono A’B”C’A”B’C”A’, los pares de lados opuestos del mismo son de la forma M’N” y M”N’ que, como hemos visto, se cortan en puntos A*, B* y C* alineados y por tanto, según el recíproco del teorema de Pascal, los seis puntos están situados sobre una cónica.

Recíprocamente, si las rectas MM’ concurren en P’, AA” y BB” en P” y si Q es el punto de encuentro de CP”con AB, por la primera parte hay una cónica que pasa por los puntos A’, B’, C’, A”, B” y Q; como bastan cinco puntos para determinar una cónica, esa cónica es la misma que la que pasa por A’, B’, C’, A”, B” y C”. El punto C” ha de ser el propio Q, pues de lo contrario la cónica y el lado AB se cortarían en 3 puntos, lo cual sólo es posible si es degenerada (producto de dos rectas), que no puede ser aquí.

En particular, están sobre una misma cónica los pies de las alturas y los puntos medios de los lados de un triángulo: es la circunferencia de Euler o de los nueve puntos (que pasa por otros tres puntos destacados).

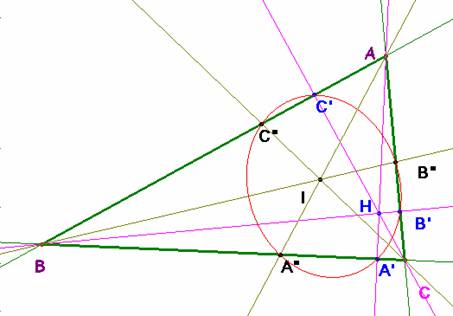
Tomando como cevianas las bisectrices y las alturas, tenemos la gráfica de la segunda figura.