Usamos la geometría
analítica y las coordenadas cartesianas. Suponemos A=(0,0), B=(0,c),
C=(0,b). |
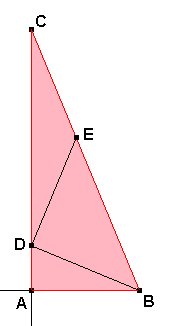
Caracterizar y construir el triángulo ABC, que es rectángulo
en A, de hipotenusa a=BC, y de catetos b=AC,
y c=AB, de tal forma que, BD=DE=EC,
donde D es un punto tomado sobre AC, E es un punto
tomado sobre BC, tal que el ángulo ÐABD=ÐACB,
y el ángulo BDE es rectángulo en D. |
|
Propuesto por Juan Bosco Romero Márquez.
|
Solución de Francisco Javier García Capitán
Usamos la geometría
analítica y las coordenadas cartesianas. Suponemos A=(0,0), B=(0,c),
C=(0,b).
La condición ÐABD=ÐACB obliga a que los triángulos ABD y ACB son semejantes.
Entonces AD : AB = AB : AC de donde AD = c^2/b. Así tenemos D=(0, c^2/b). Siendo DE perpendicular a DB, el triángulo ECD será siempre isósceles, siendo la segunda coordenada de E : (1/2)(b + c^2/b). La primera la podemos hallar teniendo en cuenta que la ecuación de la recta BC es x/c + y/b = 1. También podemos hacer:
Ahora imponemos la condición BD = DE:
A partir de aquí es fácil deducir que si b>c,
entonces la única posibilidad es que 
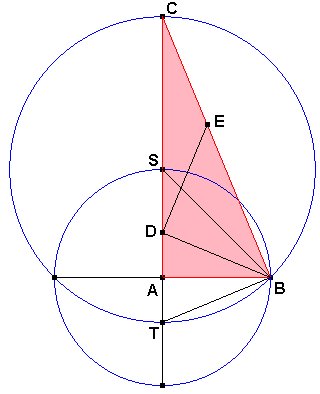Para construir este
triángulo colocamos AB=c en el eje x y trazamos
la circunferencia de centro A y radio AB que corta al eje y en S. Con
centro S y radio SB trazamos otra circunferencia que cortará en C
(por el mismo lado que S) y T (por el otro lado) al eje y. Tendremos:
Los triángulos ABD y BDE son rectángulos, así que podemos calcular R y r sabiendo que para un triángulo rectángulo con catetos x e y e hipotenusa z es R = z/2 y r = (x+y-z)/2. Así tenemos, para ABD y BDE:
Para hallar el área del triángulo DEC podemos usar las fórmulas del área del triángulo (ABC) = sr = abc/4R, con las que obtendremos:
