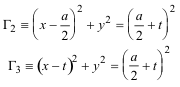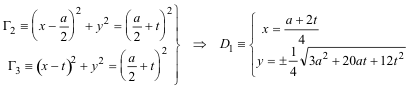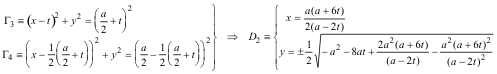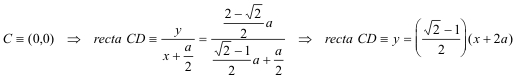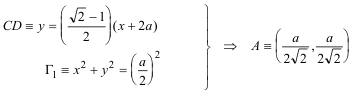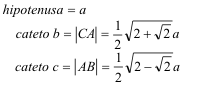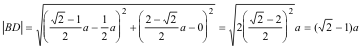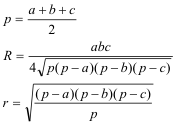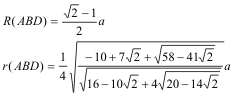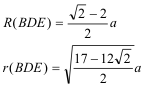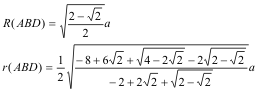De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 344 Caracterizar y construir el triángulo ABC, que es rectángulo en A, de hipotenusa a=BC, y de catetos b=AC, y c=AB, de tal forma que, BD=DE=EC, donde D es un punto tomado sobre AC, E es un punto tomado sobre BC, tal que el ángulo ABD=ACB, y el ángulo BDE es rectángulo en D.
Calculad también, los radios de los círculos inscrito y circunscrito a cada uno de los triángulos ABD, BDE, DEC.
Romero, J. B. (2006): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (21 de octubre de 2006) |
|
SOLUCIÓN |
|
Antes de empezar, prescindiremos de una de las condiciones del enunciado; porque o hay una condición de más (lo que haría insoluble el problema) o una de las condiciones es redundante (así ocurre como se ve más adelante). La condición de la que vamos a prescindir es la igualdad de ángulos
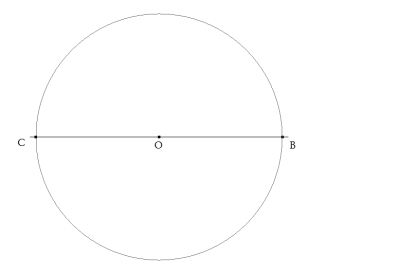
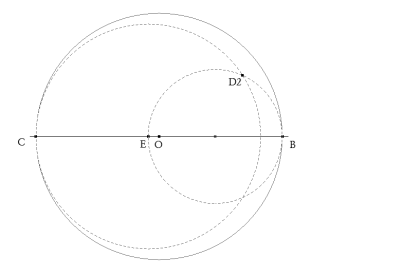
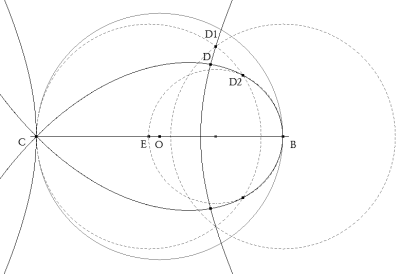
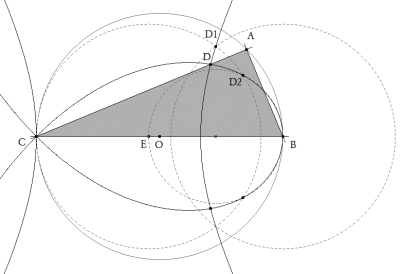
Si el triángulo BAC es rectángulo en A, la hipotenusa BC=a es el diámetro de un círculo sobre el que se halla el vértice A. Este es el círculo Γ1 cuyo centro tomamos como origen y a BC como eje de abscisas. La perpendicular a BC por el origen será el eje de ordenadas.
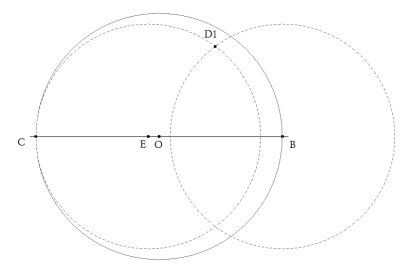
Imponemos ahora la condición BD=DE=EC. Para ello tomamos un punto cualquiera E sobre BC de abscisa t.. BD=EC significa que el punto D debería estar sobre el círculo de centro B y radio EC, es el círculo Γ2. DE=EC significa que el punto D debería estar sobre el círculo de centro E y radio EC, es el círculo Γ3.
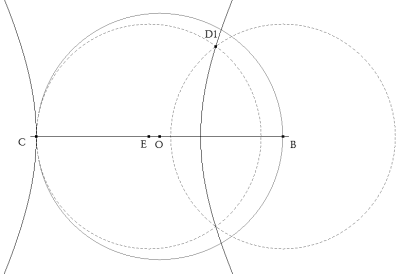
Como E es cualquiera, la intersección de Γ2 y Γ3 nos da un punto D1.
Se podría simplificar la y pero no es necesario.
Entrando con tD, por ejemplo, en D1
Sobre la recta CD
BAC es rectángulo, y por tener un lado y un ángulo común, los triángulos BAC y DAB son semejantes,
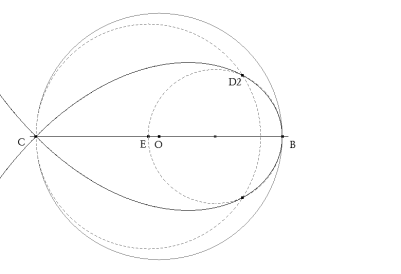
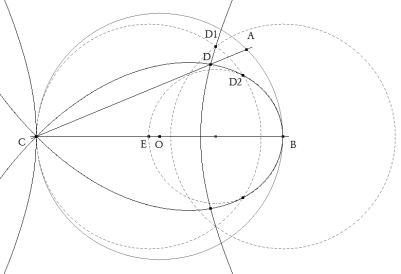
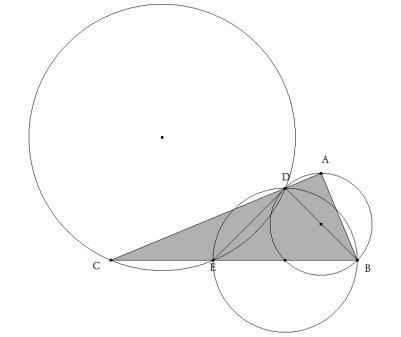
Trazamos ABC el triángulo solución que queda caracterizado del siguiente modo:
SIENDO BC LA HIPOTENUSA Y O EL PUNTO MEDIO DE BC, A ESTÁ SOBRE LA CIRCUNFERENCIA DE DIÁMETRO BC Y OA FORMA UN ÁNGULO DE Π/4 CON OB.
Calculamos ahora
junto con
y también
junto con
y los lados de los triángulos considerados son
Aunque podemos razonar sobre la figura, como tenemos la longitud de todos los lados de los triángulos considerados, usaremos las siguientes fórmulas:
TRIÁNGULO ABD
TRIÁNGULO BDE
TRIÁNGULO DEC
|