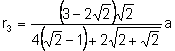Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 344
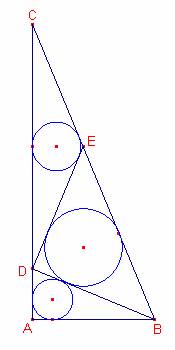
Caracterizar y construir el triángulo ABC, que es rectángulo en A, de hipotenusa a=BC, y de catetos b=AC,y c=AB, de tal forma que, BD=DE=EC, donde D es un punto tomado sobre AC, E es un punto tomado sobre BC, tal que el ángulo ABD=ACB, y el ángulo BDE es rectángulo en D.
Calculad también, los radios de los círculos inscrito y circunscrito a cada uno de los triángulos ABD, BDE, DEC.
Romero, J.B (2006): Comunicación personal.
Solución
de Ricard Peiró
i Estruch Profesor de
Matemáticas del IES 1 de Xest
(València):
Sea 
. Sea 
. Entonces, 
.
Por ser 
rectángulo 
, 
.
Por ser rectángulo y isósceles, 
, 
.
Entonces, 
, por tanto, 
.
Aplicando
el teorema de Pitágoras: 
.
Dibujar un
triángulo rectángulo con un ángulo agudo es sencillo.
Entonces, 
Aplicando
razones trigonométricas al triángulo 
:
, entonces, 
Aplicando
razones trigonométricas al triángulo rectángulo 
:
. Entonces, 
.
En un
triángulo rectángulo el radio de la circunferencia circunscrita es igual a la
mitad de la hipotenusa.
En un
triángulo rectángulo el radio de la circunferencia inscrita es igual al semiperímetro menos la hipotenusa.
Sea el
triángulo rectángulo . Sea 
el radio de la
circunferencia circunscrita y 
el radio de la
circunferencia inscrita. Entonces:
.
.
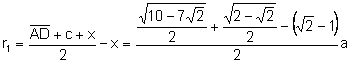Sea el
triángulo rectángulo 
. Sea 
el radio de la
circunferencia circunscrita y 
el radio de la
circunferencia inscrita. Entonces:
.
.
Sea el
triángulo 
. Sea 
el radio de la
circunferencia circunscrita y 
el radio de la
circunferencia inscrita.
Aplicando
el teorema del senos al triángulo :
. Entonces:
Aplicando
el teorema del senos al triángulo :
. Entonces: 
El área del
triángulo es, 
.
Entonces:
.
